Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 52
Se , em que é a função cujo gráfico é dado, qual dos valores seguintes é o maior?
Passo 1
Olá, meu nobre amigo, Yuri aqui e estarei te ajudando a resolver essa atividade.
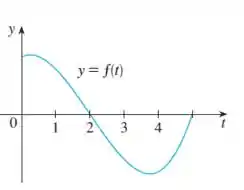
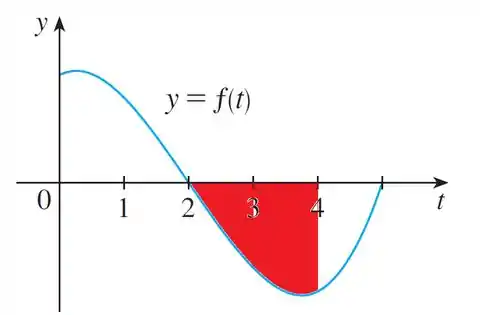
Nessa o enunciado nos dá um gráfico:
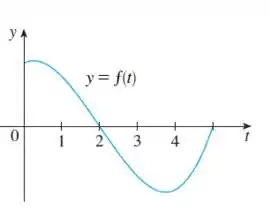
Onde sua integral pode ser calculada por:
E nos pergunta pra qual valor de é maior.
Para resolver esse problema temos que ter em mente que o módulo da integral nada mais é do que a área sobre uma curva. Se a nossa curva tiver acima do eixo a integral é positiva e se estiver abaixo ela será negativa!
Passo 2
Com a dica ali de cima ficou molezinha, né!? Temos que:
Já tirar que , como o limite inferior e superior são iguais, então . Pra analisar as próximas opções, vamos trazer o gráfico mais pra perto:
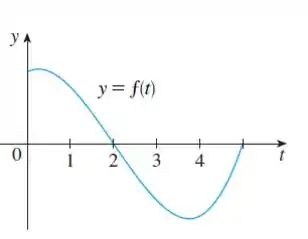
Agora olhando pra vemos que o limite de integração superior é menor do que o inferior, portanto:
O mesmo se aplica pra :
Agora sobrou
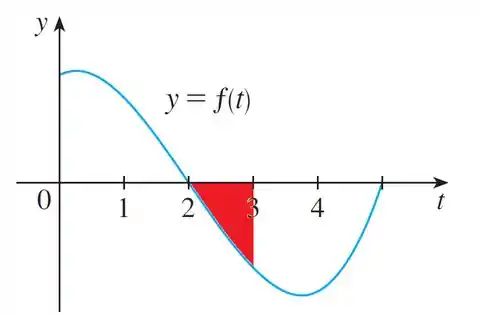
e
,
ambas são negativas. Se todos os valores são negativos, exceto , então tem o maior valor!