Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.2 - Ex. 40

A função f cujo gráfico aparece abaixo tem valores dados na tabela a seguir.

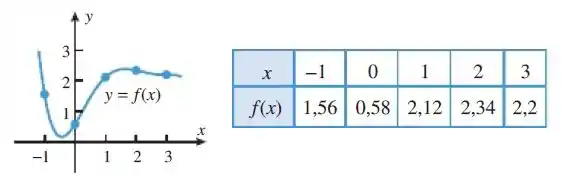
Use os dados da tabela para aproximar o valor das derivadas dadas.

  1. f ' 0,5
  2. f ' 2,5

Passo 1

  1. Para calcular f ' 0,5 a melhor aproximação deve ser usando os pontos 0 ; 0,58 e 1 ; 2,12 , assim vamos usar a fórmula abaixo para calcular a derivada em 0,5 :

    2. f ' 0,5 = f 1 - f 0 1 - 0 = 2,12 - 0,58 1 - 0 = 1,54

    Passo 2

  2. Agora para calcular f ' 2 , 5 a melhor aproximação deve ser usando os pontos 2 ; 2 , 34 e 3 ; 2,2 , assim vamos usar a fórmula abaixo para calcular a derivada em 2 , 5 :

f ' 2 , 5 = f 3 - f 2 3 - 2 = 2,2 - 2 , 34 3 - 2 = - 0 , 1 4

Resposta

  1. f ' 0,5 = 1,54
  2. f ' 2 , 5 = - 0,14
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é
Nos exercícios de 1 a 20, faça o seguinte: (a) Trace um esboço do gráfico da função; (b) determine se f é contínua em x 1 ; (c) calcule f ´ _ _ ( x 1 ) e f ´ + x 1 , se existirem, (d) determine se f é