Enunciado

Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 9

Uma função é dada por uma tabela de valores, um gráfico, uma fórmula ou por meio de descrição verbal. Determine se é injetora.

Passo 1

Eaee!!! Belezinha? Bom... a questão quer verifiquemos se a função abaixo é injetora:

Mas o que é uma função injetora?

Bom... uma função injetora é aquela que tem apenas um valor no domínio para cada valor associado no contradomínio.

Sejam e o domínio e o contradomínio, respectivamente:

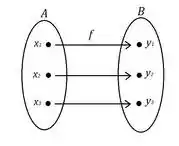
Agora que sabemos a definição, vamos aplicar!!

😉

Passo 2

Então... a expressão é uma função que descreve uma reta, pois tem uma equação do primeiro grau ali.

Dessa forma, como se trata de uma reta, temos que é impossível ter mais de um valor de para cada associado.

Dessa forma, a função é injetora!

Entendeu direitinho? Responde aee ;)

Resposta

A função é injetora

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Faça o gráfico da função f x = sin ⁡ ( sin - 1 ⁡ x ) E explique sua aparênciab) Faça o gráfico da função f x = sin - 1 ⁡ sin ⁡ x Como você pode explicar a aparência desse gráfico?

Faça o gráfico da função f x = x 3 + x 2 + x + 1 E explique por que ela é injetora. Use então um sistema de computação algébrica (SCA) para encontrar uma expressão explícita para f - 1 x . (Seu SCA va

Se g x = x 6 + x 4 , x ≥ 0 Use um sistema de computação algébrica para encontrar uma expressão para g - 1 ( x ) .Use a expressão da parte (a) para fazer na mesma tela um gráfico de y = g ( x ) , y = x

a) Se transladamos uma curva para a esquerda, o que acontece com sua reflexão em torno da reta y = x ? Em vista deste princípio geométrico, encontre uma expressão para a inversa de g x = f ( x + c ) E

Demonstre a Equação 4.