Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.6 - Ex. 5
Uma função f é dada por um gráfico. Determine se f é injetora.
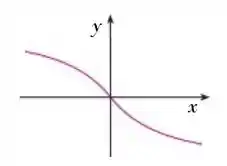
Passo 1
Bom, galera!
Queremos saber se uma função é injetora. Você lembra o que significa injetora?
Uma função injetora é uma função para cada valor no contradomínio existe apenas um valor no domínio associado.
Em outras palavras, dois pontos diferentes tem sempre imagens diferentes . Ou seja, cada tem apenas um único associado.
Olha essa representação em diagramas:
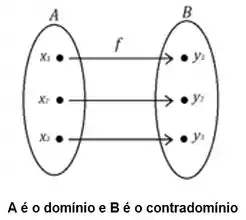
Então agora vamos olhar pra nossa . Você acha que ela é injetora? A gente tem mais de um ponto com o mesmo valor de ? Tem algum com 2 ou mais valores de ?
Existe uma técnica pra ver isso, que se chama Método da Reta Horizontal. Se você conseguir traçar qualquer reta horizontal que cruze com a curva em mais de um ponto, então a função não é injetora. Vamos aplicar no passo 2!
Passo 2
Vamos pegar como exemplo (reta azul). Não existe nenhum outro ponto de que toque nessa reta, apenas quando .
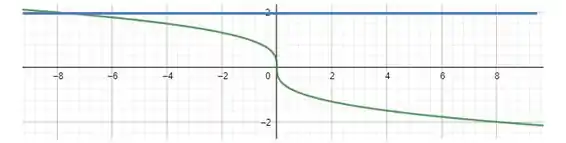
Perfeito! Mas pra gente concluir que a função é injetora, TODAS as retas horizontais precisam cruzar com a curva no máximo uma vez.
Mas só de olhar a gente vê que isso é verdade. É um possível traçar uma reta horizontal que cruze a curva 2 vezes.
Assim, todo valor do contradomínio tem apenas um valor associado no domínio . Em outras palavras, todo tem apenas um único associado.
Então a função é injetora!
Resposta
A função f é injetora.