Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 3
Uma função é dada por uma tabela de valores, um gráfico, uma fórmula ou por meio de descrição verbal. Determine se é injetora.
Passo 1
Veja bem, aqui a gente precisa responder se uma função é injetora ou não, de acordo com a forma que será nos apresentada a função.
O mais importante aqui é você ter noção do que é uma função injetora.
Uma função é chamada injetora quando ela não assume o mesmo valor duas vezes; isto é:
sempre que
Um exemplo:
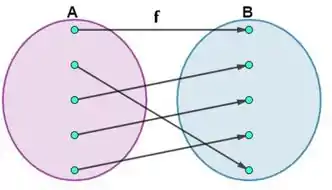
Analisando o diagrama, podemos perceber que essa é uma função injetora. Veja que não existe dois elementos do conjunto A ligados a um mesmo elemento do conjunto B, isso significa que dois elementos distintos do conjunto A sempre possuem imagens diferentes no conjunto B, o que faz com que essa função seja injetora.
Passo 2
Vemos pela tabela de valores que . Portanto, essa função não é injetora. Pois não devemos ter
Para valores
Resposta
Essa função não é injetora.