Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.8 - Ex. 30
A função definida por
é chamada de função de Bessel de ordem zero.
(a) Encontre uma função e um intervalo para o qual seja o valor médio de sobre .
(b) Dê uma estimativa para
(c) Use um CAS para traçar o gráfico de no intervalo .
(d) Dê uma estimativa para o menor zero positivo de .
Passo 1
(a)Para achar essa e esse intervalo, vamos ter que comparar a expressão de :
Com a fórmulinha para achar o valor médio de uma função num intervalo :
Queremos uma e um intervalo onde seja . Podemos escrever:
Comparando as duas expressões, vemos que os dois lados da equação vão ser iguais se:
Passo 2
(b) Para dar uma estimativa para , temos que calcular:
Vamos usar o Wolfram Mathematica para fazer essa continha. Fica assim:
A gente precisa usar a integração numérica porque essa integral não tem solução analítica. O resultado é:
Passo 3
(c) Vamos usar o Wolfram Mathematica de novo para fazer o gráfico de:
No intervalo . Fica assim:
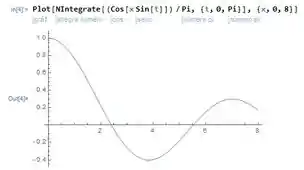
Passo 4
(d) O que ele quer é o menor valor positivo onde essa função zera. Ou seja, o ponto do lado direito do gráfico onde a função corta o eixo , e que está mais próximo da origem.
Vemos que isso acontece em um valor de um pouco maior que . Podemos usar o CAS para estimar esse valor com mais precisão, usando o comando de achar as coordenadas em um gráfico.
Fazendo isso, podemos dizer que:
Isso aí! Conseguimos!
Resposta
(a),
(b)
(c)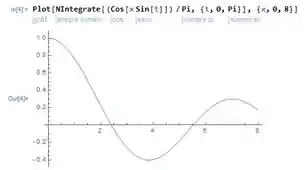 
(d)