Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 11.8 - Ex. 35

A função J I definida por

J I x = ∑ n = 0 ∞ - 1 n x 2 n + 1 n ! n + 1 ! 2 2 n + 1

é denominada função de Bessel de ordem I .

(a) Encontre seu domínio.

(b) Trace as primeiras somas parciais na mesma tela.

(c) Se seu SCA tiver funções de Bessel programadas, trace J I na mesma tela das somas parciais na parte (b) e observe como as somas parciais aproximam de J I .

Passo 1

(a) E aí, pessoal? Pra encontrar o domínio dessa função, temos que encontrar pra quais valores de x essa série converge. Então bora usar o Teste da Razão?

lim n → ∞ ⁡ a n + 1 a n = l i m n → ∞ | x 2 n + 1 + 1 | n ! n + 1 ! 2 2 n + 1 n + 1 ! n + 1 + 1 ! 2 2 n + 1 + 1 | x 2 n + 1 | = l i m n → ∞ n ! n + 2 ! 2 2 n + 1 2 2 n + 3   x 2 n + 3 x 2 n + 1 = l i m n → ∞ 1 n + 2 n + 1 2 2 x 2 = 0

Como esse limite é sempre 0 , que é menor do que 1 , a série converge pra qualquer x , ou seja, o domínio da função de Bessel é - ∞ ,   ∞ .

Passo 2

(b) Agora vamos calcular as primeiras somas parciais para poder traçá-las:

s 0 = x 2

s 1 = x 2 - x 3 2   .   2 3 = x 2 - x 3 16

s 2 = x 2 - x 3 16 + x 5 2   .   3 !   .   2 5 = x 2 - x 3 16 + x 5 384

s 3 = x 2 - x 3 16 + x 5 384 - x 7 3 ! 4 ! 2 7 = x 2 - x 3 16 + x 5 384 - x 7 18432  

s 4 = x 2 - x 3 16 + x 5 384 - x 7 18432 + x 9 4 ! 5 ! 2 9 = x 2 - x 3 16 + x 5 384 - x 7 18432 + x 9 147560

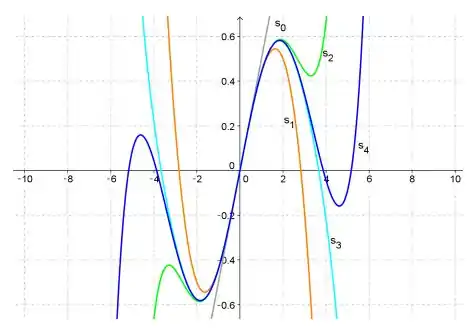
Passo 3

(c) ( S C A )

Resposta

(a) ( - ∞ , ∞ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o raio de convergência e o intervalo de convergência da série. ∑ n = 1 ∞ - 1 n x n n 2
Qual é o raio de convergência de uma série de potências? Como você o encontra?O que é o intervalo de convergência de uma série de potências? Como você o encontra?
Encontre o raio de convergência e o intervalo de convergência da série. ∑ n = 1 ∞ - 1 n n x n
Encontre o raio de convergência e o intervalo de convergência da série. ∑ n = 1 ∞ - 1 n x n n 3
Encontre o raio de convergência e o intervalo de convergência da série. ∑ n = 1 ∞ x n 2 n - 1