Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 8.4 - Ex. 6

A função demanda p s ( x ) para uma commoditie dá a relação entre o preço de venda e o número de unidades que a manufatura vai produzir naquele preço. Para um preço mais alto, manufaturas vão produzir mais unidades, então p s é uma função crescente em x . Faça com que X seja o montante de commodities que é atualmente produzido e faça com que P = p s ( X ) seja o preço atual. Alguns produtores estariam dispostos a produzir e vender a commoditie por um preço de venda menor e em troca receber mais do que seu preço mínimo. O excesso é chamando excedente de produção. Um argumento similar ao excedente de consumo mostra que o o excedente é dado pela integral:

∫ 0 X P - p s x   d x

Calcule o excedente de produção para a função demanda p s x = 3 + 0,01 x 2 em um nível de vendas X = 10 . Ilustre desenhando a curva de demanda e identificando o excedente de produção como uma área.

Passo 1

Fala aí! tudo certinho! 😉

Nesse problema foi dada uma função demanda e nosso objetivo é calcular o excedente de produção em um nível de vendas X = 10 .

Tem ideia de como fazemos isso? 😬

A primeira coisa que fazemos nesse caso é calcular a demanda P para o nível de vendas indicado...

E a partir dessa demanda fazemos

E P = ∫ 0 X P - p s x d x

Para calcular o excedente de produção...

Veja só! 😉

Passo 2

Vamos começar o exercício calculando a demanda para um nível de vendas X = 10

P = p s 10 = 3 + 0,01 10 2 → P = 4

Agora podemos calcular o excedente de produção:

E P = ∫ 0 X P - p s x d x = ∫ 0 10 ( 4 ) - ( 3 + 0,01 x 2 ) d x

Reescrevendo a integral, temos:

E P = ∫ 0 10 1 - 0,01 x 2 d x

Resolvendo a integral do passo 1, temos:

E P = x - 1 3 0,01 x 3 0 10

Substituindo os limites de integração, temos:

E P = 10 - 1 3 0,01 10 3 - 0

Simplificando a expressão...

E P = 10 - 10 3

Então o excedente de produção é:

E P = 6,67

Tranquilo até aqui? 😁

Passo 3

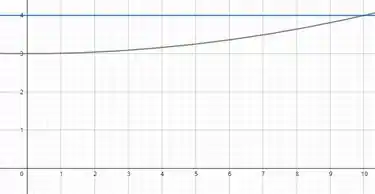
O excedente de produção é a área entre a curva de demanda e a reta que representa a demanda quando o nível de vendas é de 10 mostrado a seguir:

E aí! entendeu tudo? Responde Aí! 😉

Resposta

E P = 6,67

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a receita entra em uma companhia a uma taxa de f t = 9000 1 + 2 t , em que t é medido em anos e f ( t ) é medido em dólares por ano, encontre a receita total obtida nos primeirosquatro anos.
Se a quantidade de capital que uma companhia tem em um instante t é f ( t ) , então a derivada, f ' ( t ) , é chamada fluxo líquido de investimento. Suponha que o fluxo líquido de investimento seja t
Um cinema cobra $7,50 por pessoa e está vendendo aproximadamente 400 ingressos em uma noite típica de semana. Depois de pesquisar seus clientes, o cinema estima que, para cada 50 centavos de desconto,
A Lei da Renda de Pareto afirma que o número de pessoas com renda entre x = a e x = b é N = ∫ a b A x - k . d x , onde A e k são constantes, com A0 e k1 . A renda média destas pessoas é x - = 1 N ∫ a
A receita marginal de venda de x unidades de um produto é 12 - 0,0004 x . Se a receita da venda das primeiras mil unidades é $12400 , ache a receita de venda das primeiras 5 mil unidades.