Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.7 - Ex. 19
Para a função do exercício 18:
(a) Estime o valor de
(b)
(c) Explique.
Passo 1
Fala aí! tudo certinho? 😁
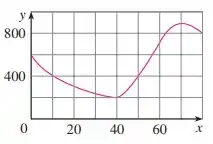
Nesse problema foi dado um gráfico de uma função e nosso objetivo é estimar , verificar se e .
Tem ideia de como fazer isso? 👀
Caso não tenha entendido, quando colocamos um tracinho em uma função , estamos na verdade falando da inclinação/taxa de variação dessa função.
Veja só! 😬
Passo 2
(a) Bom pessoal, a taxa de variação instantânea de em determinado intervalo é dada por:
Como podemos ver, tende a zero. Com o aprendido neste capítulo, esta é a definição da tangente.
Como queremos , devemos estimar o valor da tangente da curva neste ponto. Pelo gráfico, podemos estimar que a tangente em passa nos pontos e . Então:
Tranquilo até aqui? 😉
Passo 3
(b) Aqui, temos que comparar a inclinação das tangentes da curva nos pontos 10 e 30.
Aparentemente, a tangente de está mais inclinada que a tangente de . Porém, temos que observar que as tangentes estão inclinadas no sentido negativo. Portanto:
Entendeu essa parte? 😬
Passo 4
(c) para verificar se
Temos que observar novamente a inclinação para as duas condições dadas.
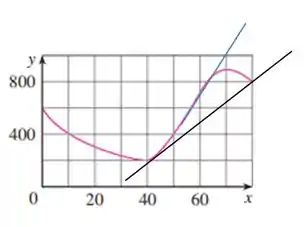
Podemos perceber claramente que a tangente em azul está mais inclinada que a preta. Então a afirmação é verdadeira.
E aí! entendeu tudo? Responde Aí! 👀
Resposta
(a)
(b)
(c)