Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 8.4 - Ex. 6
A função oferta para um produto dá a relação entre o preço de venda e o número de unidades que os fabricantes produzirão naquele preço. Por um preço maior, os fabricantes produzirão mais unidades, de modo que é uma função crescente de . Seja a quantidade de produto que é produzida atualmente e seja o preço atual. Alguns fabricantes desejariam fazer e vender o produto a um preço mais baixo e, portanto, estão recebendo mais que seu preço mínimo. O excesso é chamado excedente do produtor. Um argumento semelhante ao do excedente do consumidor mostra que o excedente é dado pela integral
Calcule o excedente do produtor para a função oferta ao nível de vendas . Ilustre desenhando a curva de oferta e identificando o excedente do produtor como uma área.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente calcular o excedente do produtor para a função oferta ao nível de vendas .
Para isso, utilizaremos a integral do excedente do produtor:
Onde é o preço de venda e é a nossa função. Depois iremos esboçar a curva de demanda e identificar o excedente como uma área.
Passo 2
Quando o nível de vendas for, temos:
O excedente, chamado de será então:
Substituindo na integral, temos:
Resolvendo a integral, obtemos o seguinte resultado:
Passo 3
Aplicando os limites de integração, temos o excedente:
E esboçando a curva graficamente, obtemos o gráfico:
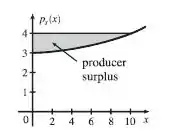
Valeu, galera! Até a próxima! 😉