Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 10.1 - Ex. 4
A função , , é tal que e para todo . Esboce o gráfico de .
Passo 1
Conforme já vimos no Exercício 1, a função que satisfaz a equação é:
onde é uma constante a ser determinada através da outra equação fornecida pelo enunciado:
Logo, será a função:
Passo 2
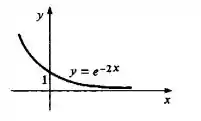
Podemos esboçar lembrando que ela é uma exponencial decrescente, com e com assíntota horizontal :
Resposta
Exercícios de Livros Relacionados
Determine a primitiva mais geral ou a integral indefinida. Confira suas respostas por diferenciação ∫ 1 - cos 6 t 2d t
Determine a primitiva mais geral ou a integral indefinida. Confira suas respostas por diferenciação ∫ 1 2 cossec 2 x - cossec x cotg x d x
Determine a primitiva mais geral ou a integral indefinida. Confira suas respostas por diferenciação ∫ 2 e x - 3 e - 2 xd x
Determine a primitiva mais geral ou a integral indefinida. Confira suas respostas por diferenciação ∫ cossec θ cotg θ 2d θ
Determine a primitiva mais geral ou a integral indefinida. Confira suas respostas por diferenciação ∫ - 5 sen ( t )d t