Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.Exercícios Práticos - Ex. 124
O gráfico abaixo, mostra o número de coelhos e de raposas em uma pequena população ártica, traçados em função do tempo durante dias.
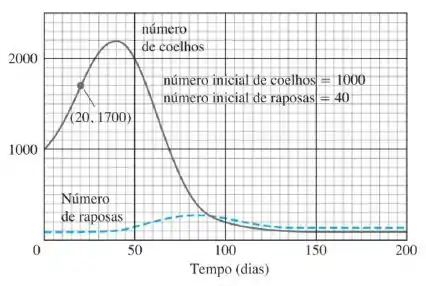
Inicialmente o número de coelhos cresceu devido à sua reprodução. Mas as raposas caçam os colehos e, como o número de raposas cresceu,o nível de coelhos estagnou, e enão caiu.
O gráfico abaixo mostra o gráfico da derivada da população de coelhos, construído com o registro dos coeficientes angulares.
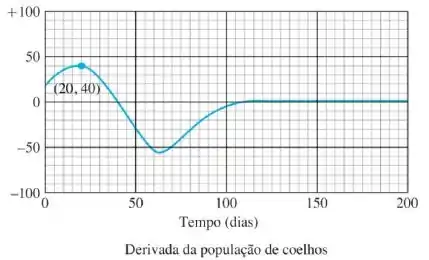
Em que unidades os coeficientes angulares das curvas das populações de coelhos e raposas deveriam ser medidos?
Passo 1
A derivada é taxa de variação certo? Aqui estamos pegando a variação no tempo.
Entao deveria ser:
E
Resposta
e
Exercícios de Livros Relacionados
( a ) Faça o gráfico da função. ( b ) Use a regra de L’Hôspital para explicar o comportamento quando x → 0 . ( c ) Estime o valor mínimo e os intervalos de concavidade. Então, use o cálculo para achar
( a ) Faça o gráfico da função. ( b ) Use a regra de L’Hôspital para explicar o comportamento quando x → 0 . ( c ) Estime o valor mínimo e os intervalos de concavidade. Então, use o cálculo para achar
Obtenha gráficos de f que revelem todos os aspectos importantes da curva. Em particular você deve usar os gráficos de f ' e f ' ' para estimar os intervalos de crescimento e decrescimento, valores ext
Obtenha gráficos de f que revelem todos os aspectos importantes da curva. Em particular, você deve usar os gráficos de f ' e f ' ' para estimar os intervalos de crescimento e decrescimento, valores ex
Obtenha gráficos de f que revelem todos os aspectos importantes da curva. Estime os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão, e use o