Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 44
Um taque reservatório de água tem o formato de um cilindro com diâmetro de m. Ele está montado de forma que as secções transversais circulares são verticais. Se a profundidade de água é m, qual porcentagem da capacidade total está sendo usada?
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui temos uma situação, onde temos um cilindro servindo de reservatório e queremos saber o seu área, para que assim podemos determinar qual a porcentagem do área total está sendo utilizado.
Aqui temos uma representação do taque:
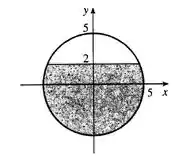
Para saber a porcentagem da capacidade total que está sendo usada devemos usar a fórmula da área utilizada sobre a área total:
Passo 2
Vamos achar a área utilizada , podemos achar através da integral:
Veja bem, vamos integrar em função da equação da circunferência, que é:
Vamos calcular em função de , assim podemos usar os limites de integração como e , como os valores de e , respectivamente, que são as retas que estão no limite da área que queremos:
Entretanto aqui vemos que corresponde apenas ao lado direito da curva, assim podemos fazer a área ser duas vezes a integral, assim pegamos a outra parte da figura:
Passo 3
Bem, agora podemos usar a Regra da Substituição Trigonométrica, vamos fazer uma mudança de variável para encontrar o valor dessa integral, e também vamos usar a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração, vemos que temos uma expressão da forma , podemos então usar a mudança de variável usando:
Vamos agora achar diferencial de , derivando:
Fazendo a substituição ficamos com:
Passo 4
Vamos calcular cada uma separadamente:
A primeira é simples, para achar as primitivas da função, vamos usar uma expressão da Tabela de Integrais Indefinidas:
Assim:
Com a segunda vamos fazer uma substituição, pois o cosseno possui uma constante dentro dele:
Derivando:
Vamos substituir:
Agora é fácil achar as primitivas da função, usando duas expressões da Tabela de Integrais Indefinidas:
Aplicando:
Juntando:
Passo 5
Não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo:
Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Vamos lá:
Passo 6
Pronto, agora é só voltar à fórmula da porcentagem da capacidade total que está sendo usada:
Resposta
A porcentagem da capacidade total que está sendo usada é de aproximadamente .