Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 3.5 - Ex. 2c

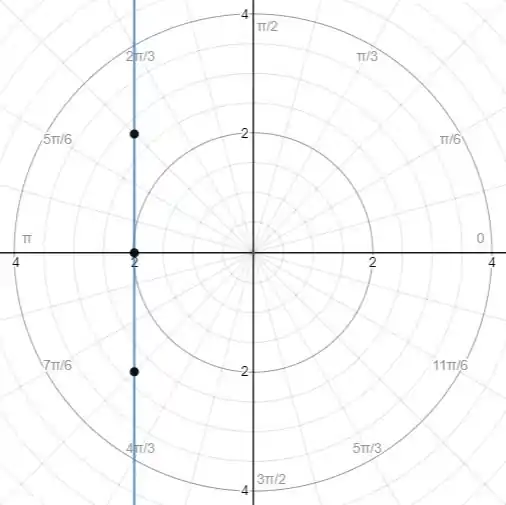
Passe a curva dada para coordenadas polares e desenhe-a.

x 2 + y 2 + x = x 2 + y 2

Passo 1

Utilizando a substituição

x = r cos ⁡ θ y = r sen ⁡ θ

Para transformar a equação para coordenadas polares

x 2 + y 2 + x = x 2 + y 2

r 2 + r cos ⁡ θ = r cos ⁡ θ + r 2 sen 2 ⁡ θ

r 2 1 - sen 2 ⁡ θ = r cos ⁡ θ - cos ⁡ θ

r = cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ

Passo 2

Antes de mais nada, vamos analisar a equação. Se - π 2 < θ < π 2 , então cos ⁡ θ > 0 e consequentemente

r = cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ = 0

Para π 2 < θ < 3 π 2 , cos ⁡ θ < 0 e

r = - cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ = - 2 cos ⁡ θ cos 2 ⁡ θ

r = - 2 cos ⁡ θ

Para os valores   π / 2 e 3 π / 2 temos uma indeterminação do tipo 0 / 0 , vamos calcular os limites

lim θ → π 2 ⁡ r = lim θ → π 2 ⁡ cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ

Analisando os limites laterais, pela esquerda

lim θ → π 2 - ⁡ cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ = lim θ → π 2 - ⁡ cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ = 0

E pela direita

lim θ → π 2 + ⁡ cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ = lim θ → π 2 + ⁡ - cos ⁡ θ - cos ⁡ θ 1 - sen 2 ⁡ θ

= lim θ → π 2 + ⁡ - 2 cos ⁡ θ 1 - sen 2 ⁡ θ

Aplicando L’Hospital

= lim θ → π 2 + ⁡ 2 sen ⁡ θ - 2 sen ⁡ θ cos ⁡ θ = lim θ → π 2 + ⁡ - 1 cos ⁡ θ = + ∞

Para 3 π / 2 temos um comportamento invertido

lim θ → 3 π 2 - ⁡ r = + ∞

lim θ → 3 π 2 + ⁡ r = 0

Passo 3

Pegando valores entre π / 2 e 3 π / 2 , montamos a tabela

Jogando os pontos no plano polar

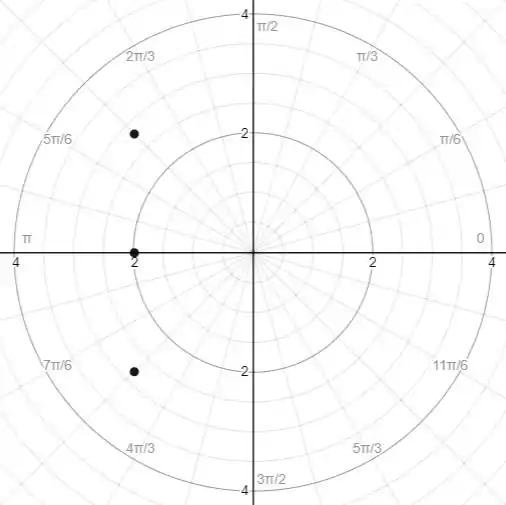
Podemos ver um padrão de uma reta e como os limites vão para o infinito, faz sentido ser uma reta.

E o gráfico da equação é

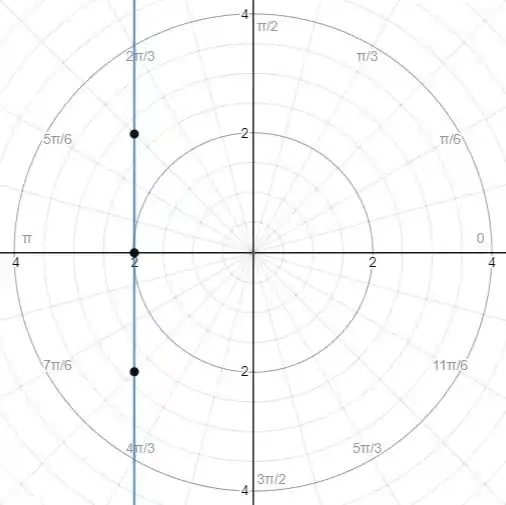
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quais das seguintes áreas são iguais? Por quê?
Calcule ∫ - 2 2 x + 3 4 - x 2 d x descrevendo-a como uma soma de duas integrais e interpretando uma dessas integrais em termos de uma área.
Encontre a área da região delimitada pela hipérbole 9 x 2 - 4 y 2 = 36 e a reta x = 3
Demonstre a fórmula A = 1 2 r 2 θ para a área de um setor circular com raio r e ângulo central θ .
Use o gráfico para aproximar as raízes da equação x 2 4 - x 2 = 2 - x . Então, aproxime a área limitada pela curva y = x 2 4 - x 2 e a reta y = 2 - x .