Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 59
Seja a reta tangente à parábola no ponto (1,1). O ângulo de inclinação de é o ângulo que faz com a direção positiva do eixo x. Calcule com a precisão de um grau.
Passo 1
Fala aí! tudo certinho? 😬
Nesse problema temos uma parábola e no ponto temos uma reta tangente que chamamos de e que forma um triangulo com o eixo e uma reta perpendicular ao eixo no ponto .
Nosso objetivo é determinar o ângulo entre e .
Parece complicado? 😁
Se esboçarmos um gráfico da função e do triangulo, ficamos com
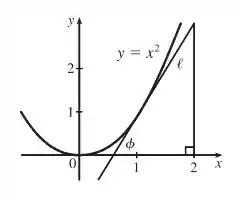
Conseguiu entender o gráfico? 😇
Passo 2
No triângulo direito no diagrama, seja o lado oposto ao ângulo e o lado adjacente ao ãngulo .
Então a inclinação da linha tangente é
Note que . Sabemos que a derivada de é .
Assim, a inclinação da tangente à curva no ponto .
Assim, é o ângulo entre e cuja tangente é 2, ou seja,
E aí! o que achou? Responde Aí! 😎
