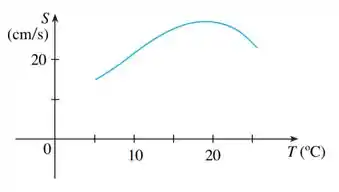
O gráfico mostra a influência da temperatura sobre a velocidade máxima de nado do salmão Coho.

1. Qual o significado da derivada ? Quais são suas unidades?
2. Dê uma estimativa do valor e de e interprete-os.

A derivada sempre representa uma taxa de variação instantânea, relacionado duas grandezas – no nosso caso, a velocidade máxima de nado do salmão e a temperatura da água.

Então, analisando as grandezas e , podemos concluir que irá representar a taxa máxima de variação da velocidade que o peixe pode atingir quando a água está a uma determinada temperatura, tranquilo?

A unidade da derivada será a unidade de dividida pela unidade de ou seja, .

Agora para calcular as estimativas das derivadas, nesse caso, temos que estimar pontos. Como o gráfico não nos dá os pontos da curva de forma precisa e nem a função que descreve a curva, o melhor que podemos fazer e verificar com uma régua ou no olhômetro mesmo pontos que nos ajudem a fazer os cálculos, beleza?

Para o caso de , aparentemente, quando temo um , o nosso fica em torno de , logo, temos o ponto . Podemos também pegar o ponto e, com esses dois, aproximar uma derivada para desse jeito aqui:

Logo, perto de uma temperatura de , a máxima velocidade do salmão muda a uma taxa de maaais ou meeenos , beleza?

Para o , podemos pegar também o ponto (aproximado) e o ponto (também aproximado). Dessa forma:

Nesse caso, a velocidade máxima do nosso salmão vai diminuindo: em torno de , essa diminuição está a uma taxa de !

Valeu, galera! Até a próxima! 😉