Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.8 - Ex. 12
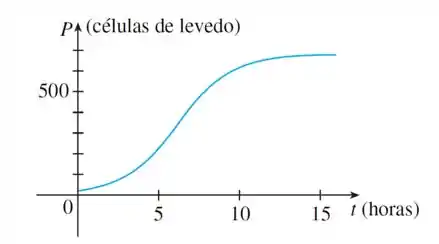
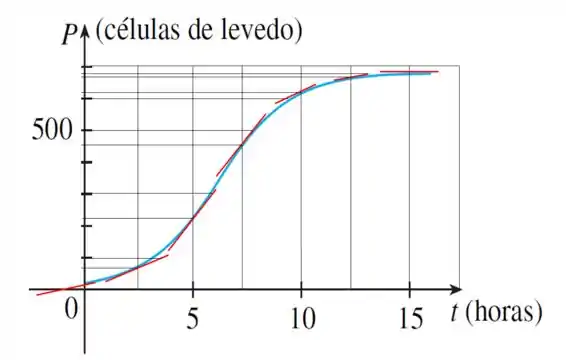
O gráfico mostrado corresponde ao da função população de cultura em laboratório de células de levedo. Use o método do Exemplo para obter o gráfico da derivada . O que o gráfico de nos diz sobre a população de levedos?
Passo 1
Opa, vamos fazer essa questão! O enunciado nos da um gráfico do crecimento de uma cultura de levedo em função do tempo:
E pede pra a gente esboçar o gráfico de a partir do gráfico de acima, usando o método do exemplo 1 do livro e depois interpretar o gráfico da derivada.
No exemplo 1 ele traça várias retas tangentes a curva, em diferentes pontos e estima o valor de suas inclinações. Como a derivada é exatamente a inclinação da reta tangente a curva em determinado ponto, tudo o que precisamos fazer é reunir esses valores e construir um novo gráfico, que será de !
Bora colocar a mão na massa?!
Passo 2
Vamos começar analisando o gráfico:
O nosso gráfico é sempre crescente, então sera sempre positivo, mas esse crescimento vai variando conforme o tempo, primeiramente o crecimento esta sempre aumentando e depois ele tende a se estabilizar até chegarmos em onde não existe mais novas células!
Devemos esperar então um gráfico de que seja crescente até atingir um máximo, depois ele irá decrecer até chegar o ponto . Agora vamos conferir se o nosso palpita ta certo!
Traçando as retas tangentes ficamos com:
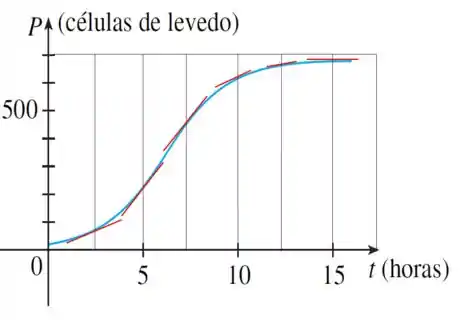
Vamos estimar, , , , , , . Vamos desenhar algumas linhas pra ajudar:
Temos que:
Onde é um outro ponto da reta tangente. Daqui pra frente teremos um trabalho bastante braçal de tentar “chutar” os pontos da melhor maneira possível! Vem comigo:
Para não precisamos nos preocupar em estimar valores porque a reta tangente tá visivelmente horizontal, então ;
Passo 3
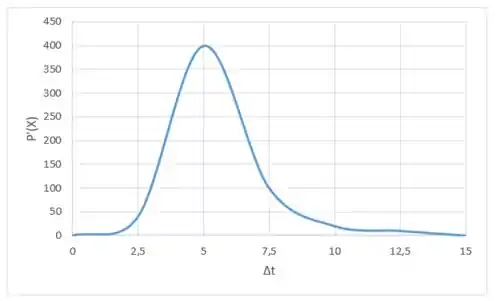
Plotando o gráfico temos:
Passo 4
Agora, precisamos analisar o que esse gráfico de significa! é a taxa de crescimento das leveduras por hora e observando o gráfico acima podemos ver que inicialmente o crescimento tem um perfil semelhante a uma função exponencial, mas depois ela atinge um máximo que significa que a taxa de crescimento começa a decrescer e finalmente o crescimento para.
Se analisarmos qual será a unidade da derivada, teremos que ela será dada em . Ou seja: teremos o quão rápido o número de leveduras irá variar em cada hora!
Resposta
Desenvolvimento acima.