Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.3 - Ex. 7

O gráfico da segunda derivada de uma função está mostrando. Diga as coordenadas dos pontos de inflexão de . Justifique sua resposta.

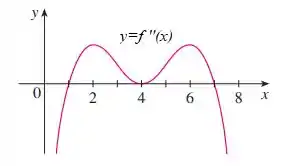
Passo 1

Eaee, belezinha?? Bom... o enunciado nos dá o seguinte gráfico que representa a derivada de uma função :

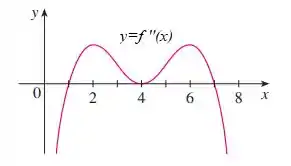
Queremos encontrar as coordenadas dos pontos de inflexão de a partir desse gráfico.

Mas o que são esses pontos??

Os pontos de inflexão são aqueles em que há troca de sinais da derivada.

Então bora analisar isso!! 😉

Passo 2

Há um ponto de inflexão em , porque muda de negativo para positivo, e a função muda de concavidade para baixo, para concavidade para cima.

Há outro ponto de inflexão em , porque muda de positivo para negativo, e a função muda de concavidade para cima, para concavidade para baixo.

Isso acontece porque quando é negativa, temos um ponto de máximo, logo, concavidade para baixo, e o contrário também é verdadeiro.

Resposta

e , porque em ambos há troca do sinal de .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que a função g x = x x tem um ponto de inflexão em 0,0 , mas g ' ' ( 0 ) não existe.

Mostre que uma função cúbica (um polinômio de terceiro grau) tem sempre exatamente um ponto de inflexão. Se seu gráfico possui três intersecções com o eixo x , x ₁ ₁, x ₂ ₂ e x ₃ ₃, mostre que a coord

Para quais valores de c o polinômio P x = x 4 + c x 3 + x 2 tem dois pontos de inflexão? E um ponto de inflexão? E nenhum? Ilustre, fazendo o gráfico de P para vários valores de c . Como o gráfico var

Use o método de Newton para encontrar as coordenadas do ponto de inflexão da curva y = e cos ⁡ x , 0 ≤ x ≤ π , com precisão de seis casas decimais.

Seja h t uma medida do conhecimento adquirido por você estudando t horas para um teste. O que você acredita ser maior, K 8 - K 7 ou K 3 - K 2 ? O gráfico de K é côncavo para cima ou para baixo? Por qu