Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.5 - Ex. 39
Os gráficos das funções nos Exercícios 39-42 possuem alguma tangente horizontal no intervalo ? Se sim, onde? Se não, por quê? Visualize os resultados representando as funções com uma ferramenta gráfica.
39.
Passo 1
Vamos calcular a derivada dessa função. Existira alguma tangente horizontal se existir um valor em que a derivada vale zero.
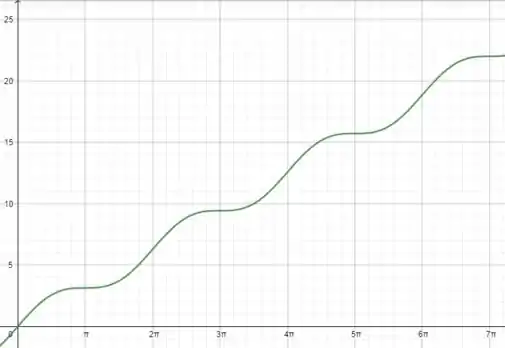
Podemos ver que a cada o gráfico volta a ter uma derivada horizontal. Portanto podemos os valores de em que a função tem derivada zero são:
onde é um número inteiro.
Resposta
Exercícios de Livros Relacionados
41-42 Ache uma equação da reta tangente à curva no ponto dado. Ilustre fazendo o gráfico da curva e a reta tangente sobre a mesma tela;42. y = x x ( 4,8 )
51. A reta normal à curva C em um ponto P é, pela definição, a reta que passa por P e é perpendicular à reta tangente a C em P. Ache uma equação da reta normal à parábola y = 1 - x 2 no ponto 2 , - 3
21-24. Encontre uma equação da reta tangente à curva dada no ponto especificado.21. y = tan x , π 4 , 1
25.(a) Encontre uma equação da reta tangente à curva y = x c o s x no ponto ( π , - π ) (b) Ilustre a parte (a) fazendo o gráfico da curva e a reta tangente na mesma tela.
O gráfico ilustra a função posição de um carro. Use a forma do gráfico para explicar suas respostas para a seguinte questão.Qual a velocidade inicial do carro?O carro está mais rápido em B ou C?O carr