Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 11.7 - Ex. 7t
t)
Passo 1
Olá, pessoal! Quando a gente olha para essa integral, a gente já pensa que não tem como resolver por substituição simples, uma vez que só temos um . Mas a malandragem aqui é usar uma identidade trigonométrica para transformar em uma função com seno e cosseno.
Essa é uma questão bem importante, pois a ideia dela serve para diversas outras! Dá uma olhada na malandragem:
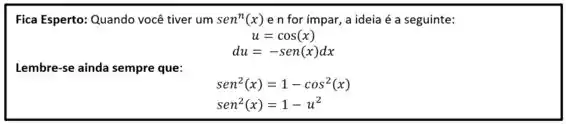
Agora vamos aplicar!
Passo 2
Então vamos começar aplicando a identidade trigonométrica,
Portanto com essa substituição, se reescrevermos a integral para:
Agora vamos fazer a substituição simples,
Vemos que podemos substituir:
Agora vamos resolver essa integral
Passo 3
Integrando,
Mas para aplicar os limites de integração, temos que voltar a integral para .
Então temos,
Agora é só finalizar!
Passo 4
Aplicando os limites de integração, temos que