Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.8 - Ex. 1

Um hemisfério e uma porção de um paraboloide são mostrados. Suponha um campo vetorial no cujas componentes tem derivadas parciais contínuas. Explique por quê.

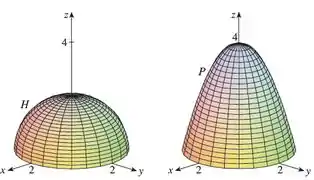
Passo 1

Faaaala galera, beleza!? Vamos começar então!

Nosso objeto é explicar porque a seguinte relação é válida:

Suponha um campo vetorial no cujas componentes tem derivadas parciais contínuas.

Onde, é um hemisfério e a porção de um paraboloide.

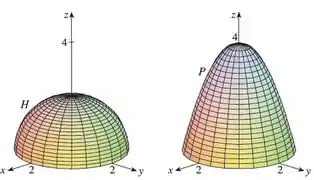
Vamos pensar juntos com calma!

Essa questão é teórica, mas nada impossível!

Vamos lembrar do Teorema de Stokes antes:

Ou seja, o Teorema de Stokes nos diz que a integral de linha em torno da curva fronteira de da componente tangencial de é igual à integral de superfície sobre da componente normal do rotacional de F.

Sabendo disso, podemos começar a analisar a questão com mais clareza.

Uma dica, observe que ambas as superfícies possuem a mesma curva C fechada.

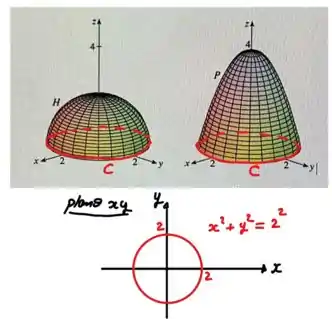
Com essas informações, ficou fácil ein!

Bora lá!

Passo 2

Agora que já analisamos as superfícies e com muita calma.

Conseguimos perceber que ambas são orientadas, suaves por partes, cujas fronteiras são formadas pela mesma curva fechada. Que podemos dizer que é orientada positiva para ambas superfícies.

Que na questão é circunferência:

Pelo teorema de Stokes, sabemos que o a integral de linha na curva fechada do hemisfério H vai ser:

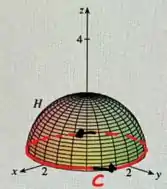
Já a integral de linha na curva fechada do paraboloide P, temos:

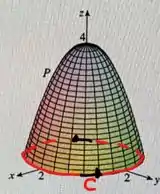
Agora consegui perceber que a curva C é a mesma para as duas regiões. Isso implica que a integral de linha vai ser a mesma para ambos os casos.

Então, e satisfazem a hipótese do Teorema de Stokes, nos levando a concluir que

Assim, demonstramos que:

Resposta

Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja S uma superfície descrita pela equação r → u . v = ( 2 . cos ⁡u . cos ⁡v , 2 . sen ⁡ u . cos ⁡v ,2 . s e n( v ) ) onde 0 ≤ u ≤ π 2 e 0 ≤ v ≤ π 2 . Esboçar a u – curva correspondente a v = π 3 e a

Seja S uma superfície descrita pela equação r → u . v = ( u . cos ⁡v , 2 u 2 ,u . s e n( v ) ) , onde 0 ≤ u ≤ 2 e 0 ≤ v ≤ 2 π . Representar graficamente a superfície S.

Seja S uma superfície descrita pela equação r → u . v = ( u . cos ⁡v , 2 u 2 ,u . s e n( v ) ) , onde 0 ≤ u ≤ 2 e 0 ≤ v ≤ 2 π . Encontrar as curvas coordenadas no ponto P 2 2 ,2 ,2 2 e representa-las

Seja S uma superfície descrita pela equação r → u . v = ( u . cos ⁡v , 2 u 2 ,u . s e n( v ) ) , onde 0 ≤ u ≤ 2 e 0 ≤ v ≤ 2 π . Determinar os vetores ∂ r → ∂ u P , ∂ r → ∂ v P , ∂ r → ∂ u P × ∂ r → ∂

Seja S uma superfície descrita pela equação r → u . v = ( 2 . cos ⁡u . cos ⁡v , 2 . s en ⁡ u . cos ⁡v ,2 . s e n( v ) ) onde 0 ≤ u ≤ π 2 e 0 ≤ v ≤ π 2 . Representar graficamente a superfície S.