Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 4a
Identificar as afirmações verdadeiras:
a) A união de bolas abertas é uma bola aberta.
Passo 1
Vamos começar vendo qual é a definição de bola aberta. Ela é uma figura que tem por equação:
Ou seja, é a parte interna de uma circunferência, sem contar a borda dela (inclusive por isso ela é um conjunto aberto).
Passo 2
Então o que a gente tem que analisar é se, juntando duas bolas abertas, a gente forma uma bola aberta. Vamos tentar resolver graficamente?
Se a gente pegar duas bolas abertas, de forma que uma esteja contida na outra, o conjunto da união delas pode ser representado só pela bola de fora, então nesse caso a união é sim uma bola aberta.
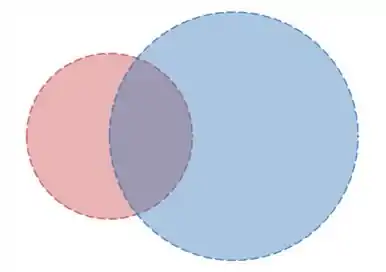
Agora, se a gente considerar duas bolas, de forma que uma não esteja totalmente contida na outra, a coisa muda: agora, o conjunto união delas deixou de ter até mesmo o formato de uma circunferência! Então, como poderia ser uma bola aberta? Portanto, como nem sempre podemos afirmar que a união vai ser uma bola aberta, essa afirmativa é falsa.
Resposta
Falsa.