Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 10a
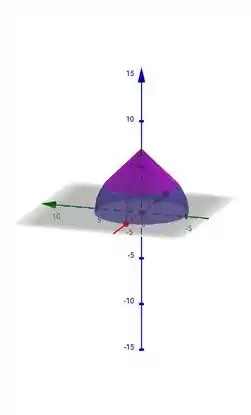
10- Considerando a função
a)Esboce o gráfico de
Passo 1
Galera, para a primeira expressão cuja nossa função está definida em circunferências que o raio varia de 0 à 4, temos o seguinte gráfico:
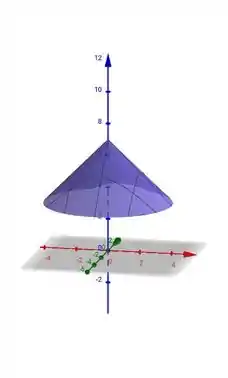
Essa superfície a gente conhece, né ?! É o nosso cone.
Passo 2
Galera, para a segunda expressão cuja nossa função está definida em circunferências que o raio varia de 4 à 5, temos o seguinte gráfico:
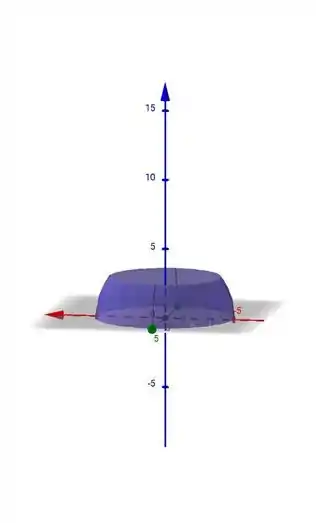
Essa superfície é meio estranha mas acho que vocês conhecem. Se:
Temos a equação da esfera, mas lembrem-se que a nossa esfera só está definida para um intervalo, por isso só temos uma parte dela, o que nos leva a obter aquela imagem meio estranha lá de cima.
Passo 3
Juntando o que obtemos nos passos anteriores, temos o seguinte gráfico para
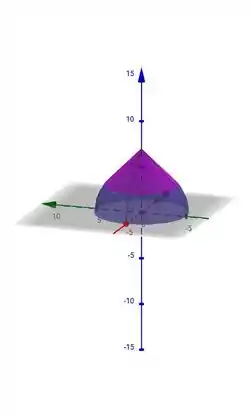
Resposta
Exercícios de Livros Relacionados
Nos exercícios 8 a 10, o conjunto S representa uma chapa plana, e T ( x , y ) , a temperatura nos pontos da chapa. Determinar as isotermas, representando-as geometricamente. S = { ( x , y ) / x 2 + y
Desenhar algumas curvas de nível e esboçar o gráfico dos seguintes parabolóides.a) z = 2 x 2 + 2 y 2
Desenhar algumas curvas de nível e esboçar o gráfico dos seguintes parabolóides.d) z = x 2 + y 2 - 1
Desenhar algumas curvas de nível e esboçar o gráfico dos seguintes parabolóides.b) z = - 2 x 2 - 2 y 2
Desenhar algumas curvas de nível e esboçar o gráfico dos seguintes parabolóides.c) z = x 2 + y 2 + 1