Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 2a
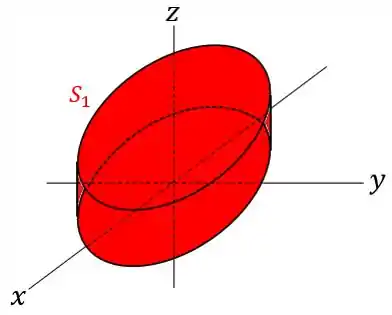
Considere a superfície , união de e , onde tem equação com , e é o gráfico da função definida no conjunto , onde .
Esboce a superfície .
Esboce a superfície .
Esboce a superfície .
Passo 1
E aí, pessoal!! Bora pra mais um exercício com o Responde Aí? Vem com a gente :D
Para a primeira parte do exercício, vamos verificar a função da superfície e ver qual forma que ela possui.
Vamos lembrar que a equação de um círculo de raio é dada por:
Passo 2
Percebemos, então, que a primeira superfície representa um círculo. Mas não é um círculo simples que está apenas em um plano bidimensional. Como nesse caso a superfície possui uma variação no eixo , então isso nos dá a informação de que essa superfície circular percorre o eixo dentro do intervalo dado. Essa variação faz com que o círculo se “estique” e vire um cilindro.
Passo 3
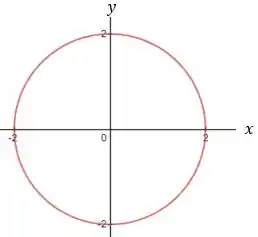
Logo, se esboçarmos a equação:
No plano em uma perspectiva bidimensional, teremos:
E passando isso para a visão tridimensional, teremos:
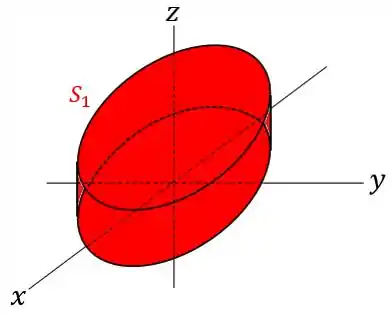
Resposta
