Enunciado

Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 2.8 - Ex. 18c

Identificar as curvas a seguir e parametrizá-las. Esboçar o seu gráfico.

c)

Passo 1

Então galerinha, o primeiro passo de todos aqui é completar os quadrados em e em para vermos o formato que que a nossa equação vai ficar, tudo bem? A equação que nos foi dada é:

Completando os quadrados, teremos o seguinte:

Pela equação que encontramos, podemos concluir que se trata de uma equação de elipse com:

Até aqui tudo tranquilão, certo? Então vamos continuar!

Passo 2

Para determinarmos uma equação vetorial, temos que lembrar que uma equação desse tipo para uma elipse é dado pela seguinte equação:

Para a nossa elipse, temos que:

Substituindo na equação vetorial, teremos:

Sendo assim, a representação paramétrica será:

Passo 3

Se esboçarmos o gráfico da elipse que encontramos, teremos o seguinte:

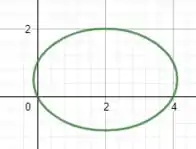
E esse é o nosso resultado, galera!

Resposta

Elipse:

Parametrização:

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboçar o gráfico da curva descrita por um ponto móvel P x ,y , quando o parâmetro t varia no intervalo dado. Determinar a equação cartesiana da curva em cada um dos itens:d) x = t + 1 ,y = t 2 + 4 ,z

Obter a equação cartesiana das seguintes curvas:b) r → t = t - 1 ,t 2 - 2 t + 2

Determinar o centro e o raio das seguintes circunferências e depois escrever uma equação vetorial para cada uma.c) x 2 + y 2 + 5 y - 2 = 0

Identificar as curvas a seguir e parametrizá-las. Esboçar o seu gráfico.a) 2 x 2 + 2 y 2 + 5 x + 2 y - 3 = 0

Verificar que a curva: r → t = 3 cosh ⁡ t i → + 5 s e n htj → É a metade de uma hipérbole. Encontrar a equação cartesiana.