1. Identifique os extremos locais de cada função nos intervalos dados e informe onde eles ocorrem
2. Esboce os gráficos da função e de sua derivada. Comente o comportamento de em relação aos sinais e valores de

Agora, vamos verificar os valores encontrados como pontos críticos, vara verificar os pontos de máximo e mínimo da função:

Logo,

:

Bom, então os valores de máximo locais são: quando e quando .

Já os valores de mínimo locais são: , quando e quando

A questão pede para comentar o comportamento da e da em seus gráficos. Primeiro observe o gráfico abaixo:

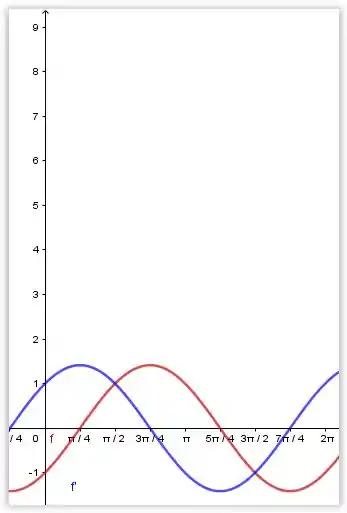
Galera, pelo gráfico acima podemos notar o seguinte: a aumenta quando e tem seus extremos locais onde . A função tem um mínimo local quando e , nesses valores a muda de negativa para positiva.

Ainda é possível perceber que a tem um valor máximo em e , nesses pontos a muda de positiva para negativa.