Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.7 - Ex. 8
Identifique a superfície de acordo com a equação dada.
Passo 1
E aí, meu povo! Tudo na boa?
Nesse exercício iremos analisar a equação:
Para identificar a superfície que a equação está descrevendo. Para isso vamos pensar no sistema de coordenas cilíndricas , e e nas suas equações.
Como o enunciado nos dá a equação em função de , vamos usar a equação do sistema de coordenadas cilíndricas:
Nesse sistema também temos para e :
Daí vamos manipular essa equação do enunciado até acharmos a superfície.
Vamos!
Passo 2
Como temos, da transformação para coordenadas cilíndricas, que:
Então, multiplicaremos a equação dada no enunciado:
nos dois lados por , obtendo:
Então, substituindo esse valor na equação da transformação de coordenadas cilíndricas, temos:
Passo 3
Sabemos ainda, que:
Sendo assim, substituindo essa relação na equação encontrada no passo 2, obtemos:
Agora, somando 1 dos dois lados da equação para completar quadrados, temos:
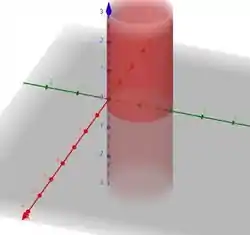
Dessa forma, temos que a superfície é um cilindro com raio 1 e deslocado de uma unidade para a direita em . Como não temos nenhuma restrição para , ele percorre todo o eixo . A imagem a seguir ilustra a superfície:
Resposta
Dessa forma, temos que a superfície é um cilindro com raio 1 e deslocado de uma unidade para a direita em . Como não temos nenhuma restrição para , ele percorre todo o eixo .