Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 6
Identifique a superfície dada a equação vetorial
Passo 1
Fala pessoal, para analisar a superfície precisamos achar a equação parametrizada para facilitar a compreensão.
Para isso vamos igualar as componentes da equação a uma função.
Sendo assim :
Para analisar a superfície vamos precisar encontrar a relação de .
Podemos ver que dependem de , logo o primeiro passo que teremos que fazer é escrever essas equações sem esse parâmetro, para podemos analisar com mais facilidade.
E analisar graficamente como elas seriam, beleza?
Passo 2
Vamos começar tirando os parâmetros das equações:
Precisamos pensar em como sumir com o parâmetro .
Uma maneira de sumir com e e tentar achar . Esse é um bizu que podemos usar em vários tipos de questões.
Bom , então vamos começar elevando cada equação ao quadrado:
Beleza , precisamos deixar o ,logo:
Somando as duas equações:
Passo 3
Beleza, já achamos que a nossa superfície tem a seguinte equação:
Bom, mas como sabemos que tipo de superfície ela será???
Olha, existem algumas equações padrões para representar superfícies. Como podemos ver, os valores que dividem e são diferentes, porém os sinais de ambos são iguais. Quando isso acontece se trata de uma elipse cilíndrica . Sua fórmula é:
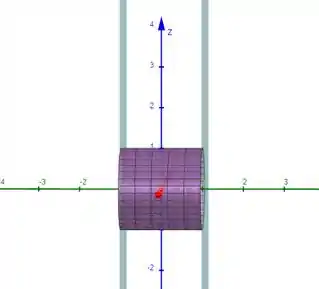
Se desenharmos o seu gráfico acharemos :
Ou seja, será um cilindro elíptico .
Porém o cilindro foi delimitado na região onde :
Como sabemos que , podemos reescrever os intervalos sendo :
Construindo o gráfico teremos :
Resposta
A superfície é um cilindro elíptico.