Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 8
Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas da grade que têm u constante e quais têm v constante.
,
Passo 1
E aiiii turminha fera, beleza!?
Nessa questão devemos plotar a seguinte superfície:
,
E avaliar as curvas na superfície, que tem constante e constante.
Para traçar o gráfico com o computador existem vários softwares. Um dos melhores para se plotar gráfico é o Geogebra 3D.
Vamos usar ele para plotar nossa superfície.
Bora lá fazer!
Passo 2
Vamos começar analisando a parametrização.
Da parametrização, temos que:
Onde,
Utilizando o Geogebra 3D, temos o seguinte gráfico:
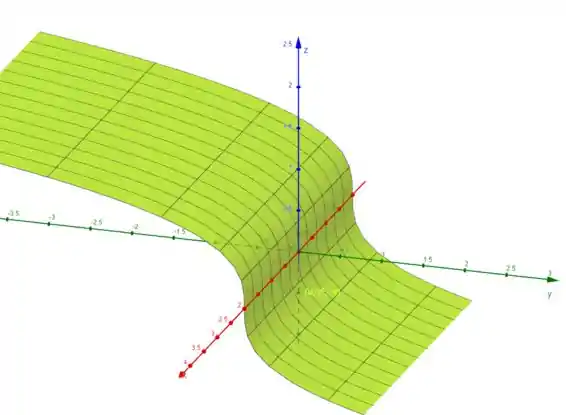
Use o seguinte input para plotar:
b=Superfície(u,v^(3),-v,u,-2,2,v,-2,2)
Passo 3
Quais são as curvas da grade que têm u constante e quais têm v constante?
Observe bem as curvas no gráfico acima.
Curvas de constante:
Estas curvas são obtidas mantendo o valor de fixo e variando .
No gráfico, as curvas de constante aparecem como linhas que se movem ao longo da direção de , que neste caso são curvas que se estendem ao longo do eixo (horizontalmente) e variam em (verticalmente).
Curvas de constante:
Estas curvas são obtidas mantendo o valor de fixo e variando .
No gráfico, as curvas de constante aparecem como linhas que se movem ao longo da direção de , que neste caso são curvas que se estendem ao longo do eixo (horizontalmente) e variam em (verticalmente).
Resposta
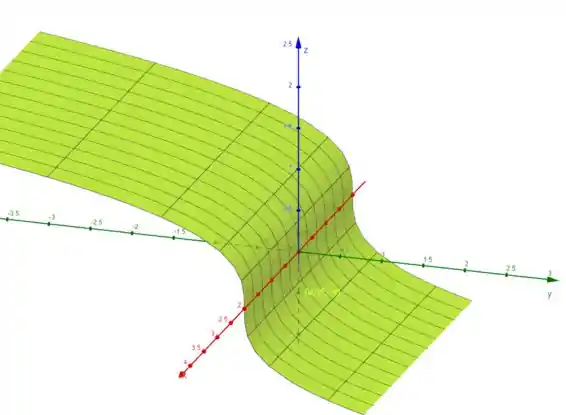
As curvas de constante são aquelas que se estendem ao longo do eixo .
As curvas de constante são aquelas que se estendem ao longo do eixo .