Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 7

Use um computador para traçar o gráfico da superfície parametrizada. Imprima o resultado e indique sobre essa impressão quais são as curvas de grade que têm u constante e quais têm v constante.

r u , v = u 2 , v 2 , u + v , - 1 ≤ u ≤ 1 ,   - 1 ≤ v ≤ 1

Passo 1

E aí, galera! Tudo na paz?

Aqui temos que usar um software para traçar o gráfico da superfície parametrizada por:

r u , v = u 2 , v 2 , u + v

Cada componente desse vetor é a parametrização de uma de nossas variáveis, então:

x = u 2  

  y = v 2

  z = u + v

Com as restrições:

- 1 ≤ u ≤ 1

E:

  - 1 ≤ v ≤ 1

Para isso, vamos usar o software GeoGebra.

Depois, vamos entender quais curvas de grade da nossa superfície tem a variável u como constante e quais tem v .

Passo 2

Usando a função superfície do GeoGebra com o seguinte input:

Conseguimos o gráfico:

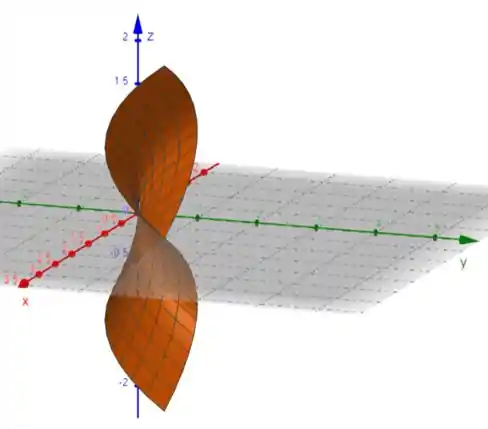
Passo 3

Entendendo as linhas de grade:

  • u constante:

    • x = u 2   (constante)

    y = v 2

    z = u + v

    Então nossas curvas vão estar no plano y z , já que x é constante.

  • v constante:

x = u 2

y = v 2 (constante)

z = u + v

Então nossas curvas vão estar no plano x z , já que y é constante

u constante

v constante

Resposta

Gráfico.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f a transformação de R 2 em R 3 dada por x , y , z = ( u + v , u , v ) . Mostre que f transforma o plano u v no plano x - y - z = 0 .
Seja f (u , v) = ( u , v , 1 - u - v ) , com u = 0 , v = 0 e u + v = 1 . Desenhe a imagem de f .
2. a. Encontre uma parametrização para a superfície obtida girando-se o circulo x - a 2 + z 2 = r 2,0ra , torno do eixo z. Esta superfície é chamada de toroB . Encontre um vetor normal a essa superfíc
1 . Seja S uma superfície parametrizada por φ u , v = v cos ⁡ u ,v s e nu , 1 - v 2 0u2 π v ≥ 0 Identifique esta superfície. Esta superfície é regular ? Trace as curvas na superfice S. Definidas por φ
3. Considere as superfícies S 1 e S 2 parametrizadas por φ 1 u , v = u , v , 0 φ 2 u , v = u 3 , v 3 , 0 u , v ∈ R 2 Respectivamente Mostre que S1 e S2 são o plano XYMostre que S1 é regular e que S3 n