Uma pedra é atirada verticalmente para cima, partindo do solo, com uma velocidade inicial de . (a) Por quanto tempo ela subirá? (b) Qual a altura máxima atingida pela pedra?

Se um objeto se move livremente numa reta vertical e está sendo puxado em direção à terra pela força da gravidad, a aceleração devido à gravidade, denotada por g m/s², varia com a distância do objeto ao centro da Terra. Entretando, para pequenas variações de distância, a aceleração, devido à gravidade, é quase constante e um valor aproximado de g, se o objeto estiver próximo ao nível do mar, será . Para esse tipo de exercício, continuam valendo as derivadas vistas para o movimento retilíneo, ou seja, .

Vamos analisar nosso exercício. Uma pedra foi lançada do solo para o alto e caiu novamente. Sabemos a velocidade com que ela sai do solo (nossa velocidade inicial no instante ). A figura a seguir ilustra a trajetória da pedra.

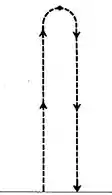
Seja t o tempo que passou desde o lançamento da pedra, s a distância percorrida pela pedra em t segundos, v a velocidade da pedra e |v| a velocidade escalar da pedra. Quando a pedra atinge o chão, . Sejam os valores do tempo e da velocidade quando a pedra atinge o chão novamente. A única aceleração presente durante todo o movimento é a da gravidade, que é vertical e aponta para baixo. A tabela a seguir apresenta as condições iniciais que temos.

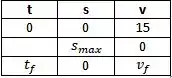
A aceleração tem um valor constante que tomaremos como . Sabendo que , temos: