Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 1.6 - Ex. 69
Se é injetora, podemos dizer algo a respeito de ? Ela também é injetora? Justifique sua resposta.
Passo 1
Fala, galera! Tudo bom?
Neste problema não tem continha, é só conceitual mesmo!
Basicamente, você tem que lembrar o que é uma função injetora: é aquela que, se você pegar 2 números diferentes, a função em cada um deles vai ser diferente. Ou seja, se para todo (domínio de ), beleza?
Então, vamos lá!
Passo 2
Aqui ele te disse que é injetora e que Repare que a diferença entre ambas é o sinalzinho de menos ali.
O que isso muda? O menos só vai fazer a função virar crescente, onde for decrescente e virar decrescente, ondefor crescente. Ou seja, vai só mexer na inclinação da função e não na função em si, certo? Então, se é injetora, também vai ser, porque a só muda a inclinação da e não muda a cara da Quer ver um exemplo?
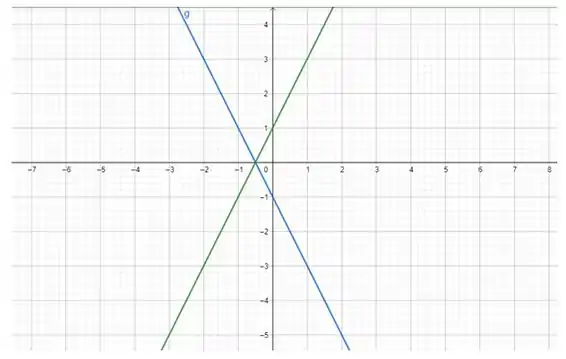
Nessa figura, a função verde é a nossa e a azul é a
Tá vendo que, em cada uma das duas funções, não existem dois que levam no mesmo ? Ambas são injetoras.
Agora olha esta outra aqui:
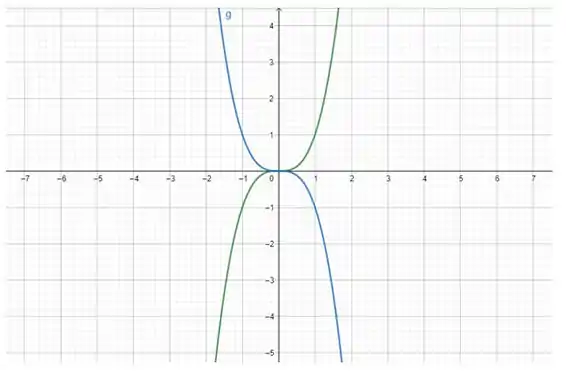
Nessa aqui, a verde é a e a azul é a
Viu só? Em nenhuma das duas funções, dois distintos levam no mesmo Ambas são injetoras.
Resposta
também é injetora.