Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.Exercícios Práticos - Ex. 106

Integrações variadas

Calcule as integrais dos Exercícios 69- 116. As integrais estão listadas de maneira aleatória.

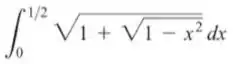
Passo 1

Para esta integral é possível resolvê-la por integração por substituição simples.

Nota-se que além dos valores da função, o intervalo de integração também deve ser substituído.

Passo 2

Com isso, pode-se fazer a substituição x = s e n u ,   t a l   q u e   d x = cos ⁡ u d u .

Para x = 0 , u = 0 ; para x = 1 / 2 , u = π / 2 .

Então:

∫ 0 1 2 1 + 1 - x 2 d x = ∫ 0 π 6 1 + 1 - s e n 2 u cos ⁡ u d u =

= ∫ 0 π 6 1 + cos ⁡ u cos ⁡ u d u

Passo 3

Uma meneira de facilitar a resolução dessa integral, um caminho possível é multiplicar a função pelo conjugado da raiz quadrada e do radicando, ou seja:

∫ 0 π 6 1 + cos ⁡ u cos ⁡ u d u   × 1 - cos ⁡ u 1 - cos ⁡ u = ∫ 0 π 6 1 - c o s 2 u 1 - cos ⁡ u cos ⁡ u d u

= ∫ 0 π 6 s e n u 1 - cos ⁡ u cos ⁡ u d u

Passo 4

Como a integral não está definida para u = 0 , deve-se aplicar o limite da integral e substituir o intervalo inferior da integral por uma constante que tende a zero. Então:

∫ 0 π 6 s e n u 1 - cos ⁡ u cos ⁡ u d u = lim t → 0 ⁡ ∫ t π 6 s e n u 1 - cos ⁡ u cos ⁡ u d u

Em seguida, a integral agora pode ser resolvida através do método da integração por partes que diz:

∫ w d v = w v - ∫ v d w

Logo, escolhendo w = c o s u ,   t a l   q u e   d w = - s e n u   d u ;   d v = s e n u 1 - c o s u d u ,   t a l   q u e   v = 2 1 - c o s u 1 / 2 , temos:

lim t → 0 ⁡ 2 cos ⁡ u 1 - cos ⁡ u 1 / 2 t π / 6 - ∫ t π 6 2 1 - cos ⁡ u 1 2 - s e n u d u ]

= lim t → 0 ⁡ 2   cos ⁡ π 6 1 - cos ⁡ π 6 1 2 - 2 cos ⁡ t   1 - cos ⁡ t 1 2 + 4 3 1 - cos ⁡ u 3 / 2 t π / 6

= lim t → 0 ⁡ 3 1 - 3 2 1 / 2 - 2 c o s t 1 - c o s t 1 / 2 + 4 3 1 - cos ⁡ π 6 3 / 2 - 4 3 1 - cos ⁡ t 3 / 2

= lim t → 0 ⁡ 3 1 - 3 2 1 / 2 - 2 c o s t 1 - c o s t 1 / 2 + 4 3 1 - 3 2 3 / 2 - 4 3 1 - cos ⁡ t 3 / 2

= 3 1 - 3 2 1 / 2 + 4 3 1 - 3 2 3 / 2 = 1 - 3 2 1 2 4 + 3 3

Portanto,

∫ 0 1 2 1 + 1 - x 2 d x = 4 + 3 2 - 3 3 2

Resposta

4 + 3 2 - 3 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral26. ∫ cot ⁡ 3 x d x
Calcule a integral30. ∫ tan 5 ⁡ x sec 4 ⁡ x d x
Calcule a integral32. ∫ tan 4 ⁡ θ sec 4 ⁡ θ d θ
Calcule a integral22. ∫ 0 2 π sin 2 ⁡ k x d x
Calcule a integral19. ∫ 0 π / 3 sin 4 ⁡ 3 x cos 3 ⁡ 3 x d x