Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.1 - Ex. 10
O mapa de contorno mostra a temperatura, em graus Fahrenheit, às horas da tarde do dia de fevereiro de , no estado do Colorado. (O estado mede mi de leste a oeste e mi de norte a sul.) Utilize a Regra do Ponto Médio com para estimar a temperatura média do Colorado nessa hora.
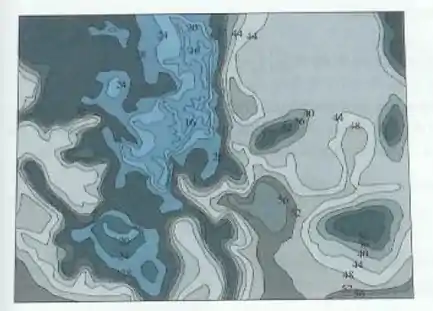
Passo 1
Temos que para estimar o valor médio de usamos:
Vamos primeiro usar a regra do ponto médio para calcular a integral, temos que os pontos do intervalo utilizado vão ser o ponto médio de cada intervalo, temos que , vamos calcular , temos que a área total da região é:
Então:
Então usando a soma de Riemann para estimar a integral temos:
Passo 2
Agora podemos estimar o valor médio de :
Resposta
Exercícios de Livros Relacionados
Calcule as integrais, para as regiões D indicadas.(c) int int_D (x + 2 y) d x d y ; D l i m i t a d a p o r y = x^(- 2) , y = 1 e y = 4
Transforme a soma das integrais duplas ∫ - 1 0 ∫ - x + 1 x + 1 f x ,y d y d x + ∫ 0 1 ∫ - 1 - x 1 - x f x ,y d y d x Em uma única integral dupla numa região D conveniente.
Calcule as integrais, para as regiões D indicadas.(b) int int_D cos (y^3) d x d y ; D l i m i t a d a p o r y = sqrt(x) , y = 2 e x = 0
As integrais abaixo não podem ser calculadas exatamente, em termos de funções elementares, com a ordem de integração dada. Inverta a ordem de integração e faça os cálculos. b∫ 0 1 ∫ x 1 s e n y y d y
Determine a região de integração D e troque a ordem de integração das seguintes integraisa. ∫ 0 1 ∫ x 3 x f x , y d y d x