Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 28

Use o roteiro dessa seção para esboçar a curva:

y = x 2 - x ²

Passo 1

Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui iremos esboçar o gráfico da função dada a partir do roteiro dado pela seção.

Nós temos a função y = f x = x 2 - x 2

Para iniciar a questão vamos relembrar um pouco da teoria:

Domínio: Conjunto de todos os valores de (   x   ) para os quais a função f x é definida.

Interseções com os Eixos:

- Eixo x : Onde (   f ( x )   =   0   ) .

- Eixo y : Onde (   x   =   0   ) , ou seja, f ( 0 )

Simetria:

- Função Par: (   f - x =   f x ) .

- Função Ímpar:   (   f - x =   - f x ) .

Assíntotas:

- Assíntotas Verticais: Linhas verticais onde a função cresce sem limites.

- Assíntotas Horizontais: Linhas horizontais que a função se aproxima conforme (   x → ± ∞ ) .

Derivadas e Comportamento da Função:

- Primeira Derivada f ' x : Para determinar onde a função é crescente ou decrescente.

- Segunda Derivada f ' ' x : Para determinar a concavidade e pontos de inflexão.

Concavidade e Pontos de Inflexão:

- Concavidade para cima: (   f ' ' x >   0   ) .

- Concavidade para baixo: (   f ' ' x <   0   ) .

- Pontos de Inflexão: Onde (   f ' ' x =   0   )   e muda de sinal.

Passo 2

  1. Nosso primeiro passo é calcular o domínio. Como nossa raiz não pode ser negativa, temos que:

    2. 2 - x ² ≥ 0

    2 ≥ x ²

    x ² ≤ 2

    x ≤ ± 2

    Assim, o domínio é x     x ≤ ± 2 } = [ - 2 , 2 ] .

  2. Agora precisamos achar os interceptos. Intercepto y : f 0 = 0 ; intercepto x : f x = 0 , então: x 2 2 - x ² = 0 → x = 0 ou x = ± 2 .

  3. f - x = - f ( x ) , então f é uma função ímpar e é simétrica a partir da origem.

  4. Não há assíntotas.

    5. Passo 3

  5. Encontrando os intervalos de crescimento e decrescimento:

    6. f ' x = x - x 2 - x 2 + 2 - x 2

    = - x 2 + 2 - x 2 2 - x 2

    = 2 1 + x 1 - x 2 - x 2

    f ' ( x ) é negativa para - 2 < x < - 1 e 1 < x < 2 , e positiva para - 1 < x < 1 , logo, é decrescente em ( - 2 , - 1 ) e ( 1 , 2 ) e crescente em ( - 1,1 ) .

  6. Valor de mínimo local: f - 1 = - 1 . Valor de máximo local: f 1 = 1 . Isso acontece porque ela decresce até - 1 e começa a cresce até 1 , depois decresce novamente.

    7. Passo 4

  7. Achando concavidades e pontos de inflexão por meio da derivada segunda:

    8. f ' ' x = 2 - x 2 - 4 x - 2 - 2 x 2 - x 2 - x 2 2 - x 2 1 2 2

    f ' ' x = 2 - x 2 - 4 x + 2 - 2 x 2 x 2 - x 2 3 2

    = 2 x 3 - 6 x 2 - x 2 3 2

    = 2 x x 2 - 3 2 - x 2 3 2  

    Desde que x 2 - 3 < 0 para x em [ - 2 , 2 ] , f ' ' x > 0 para - 2 < x < 0 e f ' ' x < 0 para 0 < x < 2 .

    Assim, sabemos que f é côncava para cima em ( - 2 , 0 ) e côncava para baixo em 0 , 2 . Há um ponto de inflexão em ( 0,0 ) , que é onde a derivada troca o sinal.

    Passo 5

  8. Esboço da função:

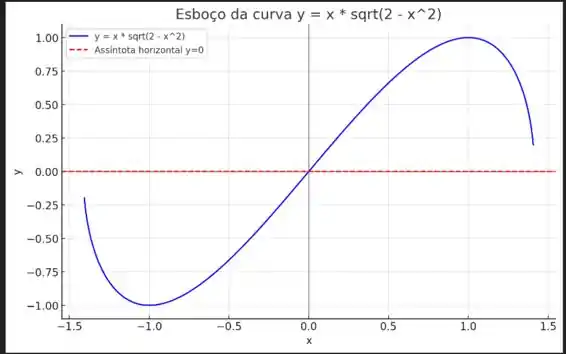
-Domínio: A curva está definida apenas no intervalo - 2 , 2

- Interseções com os Eixos: A curva intercepta os eixos (   x   )   e   (   y   ) nos pontos

- 2 , 0 ,   0,0 ,   e   ( 2 , 0 ) .

- Simetria: A função é ímpar, o que significa que o gráfico é simétrico em relação à origem.

- Assíntotas: Não existem assíntotas verticais ou horizontais.

- Pontos Críticos: Os pontos (   x   =   ±   1   ) são críticos, indicando mudanças no comportamento da curva.

- Concavidade e Pontos de Inflexão: A análise da segunda derivada indicou um ponto de inflexão em (   x   =   0   ) .

O gráfico confirma as propriedades e características analisadas da função

y = x 2 - x ²

Mostrando seu comportamento dentro do domínio permitido.

Resposta

Vide o passo a passo.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

(a) Encontre as assíntotas vertical e horizontal.(b) Encontre os intervalos nos quais a função é crescente ou decrescente.(c) Encontre os valores máximos e mínimos locais.(d) Encontre os intervalos de
(a) Encontre as assíntotas vertical e horizontal.(b) Encontre os intervalos nos quais a função é crescente ou decrescente.(c) Encontre os valores máximos e mínimos locais.(d) Encontre os intervalos de
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf
(a) Encontre os intervalos em que a função é crescente ou decrescente.(b) Encontre os valores máximos ou mínimos locais.(c) Encontre os intervalos de concavidade e os pontos de inflexão.(d) Use as inf