Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 25

Use o roteiro dessa seção para esboçar a curva:

y = (x)/(sqrt(x^2 + 1))

Passo 1

Nós temos a função y = f (x) = (x)/(sqrt(x^2 + 1))

Passo 2

  1. Nosso primeiro passo é calcular o domínio. Nossa raiz precisa ser maior que zero, pois além de ser raiz, está na parte de baixo da fração, assim, mas como temos x^2 + 1 dentro dela, ela nunca será negativa, então nosso domínio são reais. D = R .

  2. Agora precisamos achar os interceptos. Intercepto y : f (0) = 0 ; intercepto x : f (x) = 0 , então: (x)/(sqrt(x^2 + 1)) = 0 , x = 0 .

  3. f (- x) = - f ( x ) , então temos uma função ímpar, e a curva é simétrica em relação à origem.

  4. Temos que:

    5. underset(x -> oo)(lim) (x)/(sqrt(x^2 + 1)) = underset(x -> oo)(lim) ((x)/(x))/((sqrt(x^2 + 1))/(x)) = underset(x -> oo)(lim) ((x)/(x))/((sqrt(x^2 + 1))/(sqrt(x^2))) = underset(x -> oo)(lim) (1)/(sqrt((1 + 1)/(x^2))) = (1)/(sqrt(1 + 0)) = 1

    Além disso, temos:

    underset(x -> - oo)(lim) (x)/(sqrt(x^2 + 1)) = underset(x -> - oo)(lim) ((x)/(x))/((sqrt(x^2 + 1))/(x)) = underset(x -> - oo)(lim) ((x)/(x))/((sqrt(x^2 + 1))/(- sqrt(x^2))) = underset(x -> - oo)(lim) (1)/(- sqrt((1 + 1)/(x^2))) = (1)/(- sqrt(1 + 0)) = - 1

    Assim, em y = +- 1 temo uma assíntota horizontal.

  5. Encontrando os intervalos de crescimento e decrescimento:

    6. f (x) = (x)/(sqrt(x^2 + 1))

    f^' (x) = (sqrt(x^2 + 1) - x (2 x)/(2 sqrt(x^2 + 1)))/([ (x^2 + 1)^((1)/(2)) ] ²) = (x^2 + 1 - x^2)/((x^2 + 1)^((3)/(2))) = (1)/((x^2 + 1)^((3)/(2))) > 0

    f é maior que zero para qualquer x , assim, f é crescente em R .

  6. Como a função apenas cresce, não há valores extremos.

  7. Achando concavidades e pontos de inflexão por meio da derivada segunda:

    8. f^(' ') (x) = - (3)/(2) (x^2 + 1)^(- (5)/(2)) 2 x = - (3 x)/((x^2 + 1)^((5)/(2)))

    Sendo assim, temos que f^(' ') (x) > 0 para x < 0 , e f^(' ') (x) < 0 para x > 0 . Assim, temos que f é côncava para cima em ( - oo , 0 ) e côncava para baixo em ( 0 , oo ) . Há um ponto de inflexão em ( 0,0 ) , que é onde a derivada troca o sinal.

    Passo 3

  8. Esboço da função:

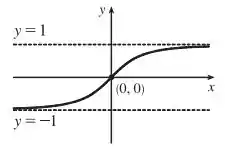
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use o roteiro desta seção para esboçar a curva.y = e^(- x) s e n x , 0x(pi)/(2)
O gráfico da função velocidade de um carro está mostrado na figura. Esboce o gráfico da função posição.
Trace um gráfico de f e use-o para fazer um esboço da primitiva que passe pela origem. f x = s e nx 1 + x 2 , - 2 π ≤ x ≤ 2 π
Trace um gráfico de f e use-o para fazer um esboço da primitiva que passe pela origem. f x = x 4 - 2 x 2 + 2 - 1 , - 1,5 ≤ x ≤ 1,5
( a ) Use uma ferramenta gráfica para fazer o gráfico de f x = 2 x - 3 x . b Começando com o gráfico da parte a , esboce um gráfico da primitiva F que satisfaça F 0 = 1 . ( c ) Use as regras dessa seç