Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 5.4 - Ex. 70
Lake Lanier na Geórgia, EUA, é um reservatório criado por Buford Dam no rio Chattahoochee. A tabela mostra a taxa de entrada de água, em pés cúbicos por segundo, conforma medido todas as manhãs às da manhã pelo Corpo do Exército de Engenheiros dos EUA. Use a regra do ponto médio para estimar o valor de água que chegou ao lago Lanier a partir de de julho de às am até de julho às am.
Passo 1
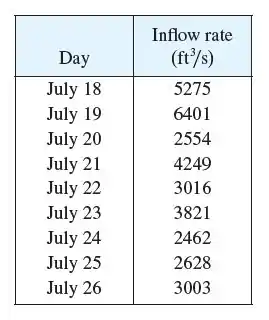
Pessoal, nessa questão temos o fluxo de água, em pés cúbicos por segundo, que chega no lago Laniear e foi medido todo dia às 7:30 da manhã e apresentado na seguinte tabela.
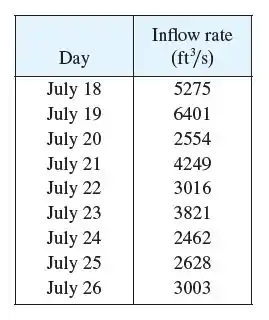
A questão pede para encontrarmos uma estimativa usando pontos médios, para encontrar qual quantidade de água chegou no lago entre os dias 18 de Julho e o dia 26 de Julho.
Temos que a regra do ponto médio é dada por:
Dessa forma, o que vamos fazer aqui é usar o valor da taxa média entre dois dias consecutivos (daí a ideia de ponto médio) e multiplica-la pelo que é o intervalo (nesse caso de tempo) entre um ponto de medição e outro.
Como a taxa está em segundos, esse intervalo de tempo deve ser calculado em segundos também, de forma que teremos:
E como esse cara é constante ele pode sair do somatório:
Passo 2
Vamos lá, vamos encontrar uma estimativa usando pontos médios, dessa forma, a variação média de entrada de água entre dois dias consecutivos é dada por:
Dessa forma, teremos:
Pronto, temos então que a estimativa do valor de água que chegou ao lago Lanier a partir de de julho de às am até de julho às am é de .