Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 49
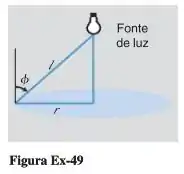
Uma lâmpada é suspensa acima do centro de uma mesa circular de raio . A que altura acima da mesa ela deve ser colocada para se obter o máximo de iluminação na borda da mesa? [Suponha que a iluminação seja diretamente proporcional ao cosseno do ângulo de incidência dos raios de luz e inversamente proporcional ao quadrado da distância da fonte de luz (Figura Ex-49).]
Passo 1
Então pessoal, o enunciado nos diz para supor que a iluminação seja diretamente proporcional ao cosseno do ângulo de incidência dos raios de luz e inversamente proporcional ao quadrado da distância da fonte de luz, assim como mostrado na figura da questão. Escrevendo isso, teremos:
Aqui é uma constante de proporcionalidade qualquer, tudo jóia? Show! Ademais, pelo triângulo retângulo da figura, temos que a altura da mesa até a fonte de luz é:
E também, pelo teorema de Pitágoras:
Substituindo tudo isso na expressão de , teremos:
Show!
Passo 2
Estabelecemos uma função de , uma vez que o raio é constante aqui pra gente! Como queremos a altura para que a iluminação seja máxima, então:
Agora igualando nossa derivada a zero para determinarmos os pontos críticos da função, teremos:
Isso só é zero se:
E essa é a altura necessária para ser máximo, galera! 😉