Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.7 - Ex. 35
Uma lata cilíndrica sem o topo é feita para receber de líquido. Encontre as dimensões que minimizarão o custo do metal para fazer a lata.
Passo 1
Eaee, belezinha??? Bom... o enunciado nos diz que uma lata cilíndrica sem o topo é feita para receber de líquido.
Queremos calcular as dimensões que minimizarão o custo do metal para fazer a lata.
Para isso, temos que relacionar de alguma forma a área superficial com o volume do cilindro.
Depois, para minimizar, devemos igualar a zero a derivada da expressão que a gente encontrar para encontrarmos as dimensões.
Mas antes, vamos esboçar o desenho de um cilindro de raio e altura :
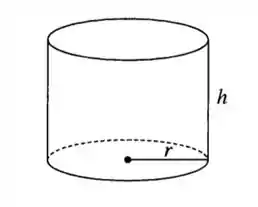
Passo 2
Bom... a área superficial total é dada pela parte lateral do cilindro (que é um retângulo de área ) e a parte de baixo (que é um círculo de área ).
Assim, somando, temos:
Dentro dessa lata precisamos conseguir colocar um volume , que tem por fórmula:
Com a fórmula do volume conseguimos isolar uma das variáveis para facilitar a nossa resolução e a vida:
Substituindo na fórmula do volume:
Agora vamos derivar e igualar a zero para minimizar!!
Passo 3
Minimizando , podemos encontrar o menor raio:
Passo 4
Substituindo em , podemos encontrar a menor altura:
Resposta
Raio:
Altura: