Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.1 - Ex. 1
(a) Lendo os valores do gráfico dado de , utilize cinco retângulos para encontrar as estimativas inferior e superior para a área sob o gráfico dado de de até . Em cada caso, esboce os retângulos que você usar.
b) Encontre novas estimativas, usando dez retângulos em cada caso.
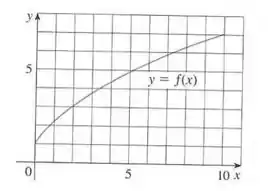
Passo 1
E aí, galerinha!
Nesse problema temos uma curva dada por
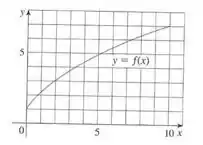
Nosso objetivo é estimar a area abaixo da curva utilizando estimativas superiores e inferiores para a) 5 retângulos e b) 10 retângulos.
Tem ideia de como fazemos isso?
Para fazer essas estimativas, dividimos nossa região em retângulos e somamos cada area de retângulo.
A área de um retângulo é dado por:
Onde a base será a variação em e a altura será o valor da função calculada no menor para a estimativa inferior e no maior para a estimativa superior.
Veja só!
Passo 2
Primeiro encontraremos a estimativa inferior, que podemos visualizar no seguinte gráfico:
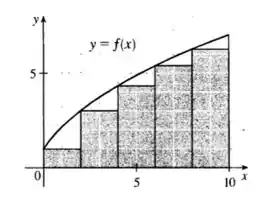
Como está crescendo, podemos obter essa estimativa inferior usando as extremidades esquerdas. Nós precisamos usar retângulos, então nosso , logo:
Nosso é:
Logo, é:
Tranquilo até aqui?
Passo 3
Agora, encontraremos as estimativas superiores, cujo esboço é o seguinte gráfico:
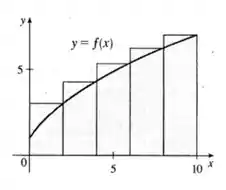
Com crescendo, podemos usar as extremidades direitas, então:
Comparando com , vemos que nós adicionamos a área acima do retângulo mais à direita, , e subtraímos a área abaixo do triângulo mais à esquerda, .
Show?
Passo 4
Agora faremos a mesma coisa utilizando .
Fazendo primeiro a estimativa inferior, temos que:
Encontramos os valores de pelo seguinte gráfico esboçado com as estimativas inferiores:
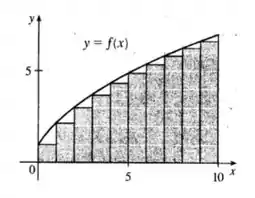
Bacana, não é?
Passo 5
Agora para as esmativas inferiores temos o gráfico seguinte:
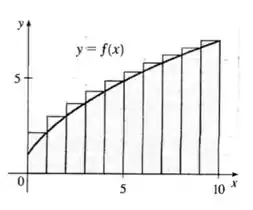
O que fizemos acima foi a comparação feita no passo 2, somamos o retângulo mais à direita, que não é utilizando em , e subtraímos o retângulo mais à esquerda, que é utilizando em mas não em .
E aí! entendeu tudo? Responde Aí!
Resposta
- e
- e