Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.2 - Ex. 21
Use um gráfico para estimar as coordenadas do ponto extremo esquerdo na curva , . Então use o cálculo para encontrar as coordenadas exatas.
Passo 1
Opa, tudo tranquilo? Questãozinha de curva paramétrica, vamos lá!
O problema nos dá as equações paramétricas de uma curva
E nos pede para encontrar o ponto mais à esquerda de duas formas: estimando pelo gráfico e usando cálculo!
Dessa forma, para o primeiro caso, só precisamos plotar o gráfico em algum software (recomendo o GeoGebra) e estimar o ponto!
Dessa forma, obtemos a seguinte curva
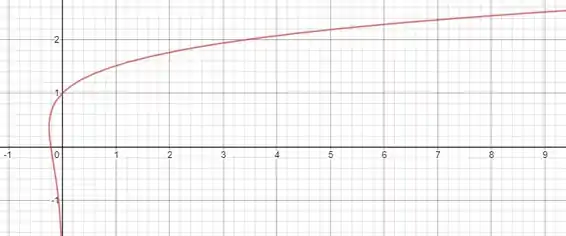
E nela nós já conseguimos identificar o ponto extremo à esquerda de cara!
Mas e como encontramos esse ponto usando cálculo? Observe que, se temos um ponto extremo à esquerda, esse ponto sempre vai ter uma reta tangente vertical! Tipo assim:
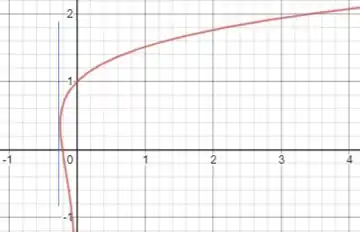
E se a reta é vertical isso significa que sua inclinação é “infinita”! E como essa inclinação é dada por
Para que tenda ao infinito precisamos que
Com isso nós vamos conseguir encontrar o ponto exato que estamos buscando!
Passo 2
Temos o seguinte gráfico
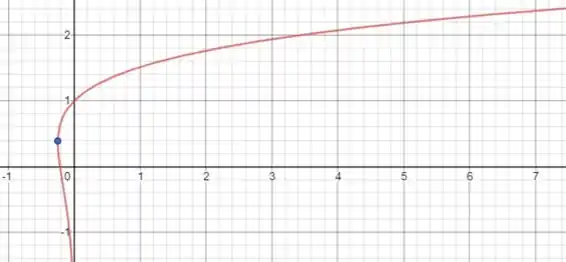
De forma que podemos aproximar o ponto extremo esquerdo por
Passo 3
No ponto extremo temos que
Onde
Resolvendo a equação encontramos o valor de
Como
Assim, substituindo esse valor nas expressões paramétricas
Desta forma, o ponto pedido tem coordenadas