Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 1.2 - Ex. 39

Seja

f (x) = (x^3 - 1)/(x - 1)

(a)Encontre underset(x -> 1)(lim) f ( x )

(b)Esboce o gráfico de y = f ( x )

Passo 1

(a)Pra calcularmos esse limite, temos que trabalhar em cima desse quociente, já que aplicando diretamente 1 em x , chegaríamos à indeterminação (0)/(0) .

Fazemos isso pelos nossos conhecimentos de produtos notáveis. O numerador, do tipo a^3 - b^3 , pode ser reescrito da seguinte forma:

underset(x -> 1)(l i m) (x^3 - 1)/(x - 1) = underset(x -> 1)(l i m) (( x - 1 ) ( x^2 + x + 1 ))/(x - 1) =

= underset(x -> 1)(l i m) ( x^2 + x + 1 )

Agora, sim, podemos aplicar o valor do limite:

underset(x -> 1)(l i m) (x^2 + x + 1) = 1^2 + 1 + 1 = 3

Passo 2

(b)Temos o gráfico de f ( x ) :

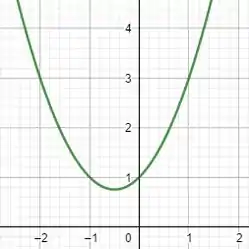
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Demonstre cada afirmação usando a definição ϵ , δ de limite. lim x → a ⁡ x = a
Demonstre cada afirmação usando a definição ϵ , δ de limite. lim x → 0 ⁡ x 3 = 0
Esboce o gráfico de um exemplo de uma função f que satisfaça todas as condições dadas f 0 = 0 f 1 = 1 lim x → ∞ ⁡ f ( x ) = 0 féi m p a r é
Encontre o limite ou demonstre que não existe. lim x → ∞ ⁡ e - 2 x cos ⁡ x
Fazendo os gráficos de y = e - x 10ey = 0,1 na mesma tela, descubra quão grande você precisará tornar x para que e - x 100,1 A parte (a) pode ser resolvida sem usar uma ferramenta gráfica?