Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 8
Para o limite
ilustre a Definição encontrando os valores de que correspondam a e .
Passo 1
Opa, vamos fazer essa questão! Temos o seguinte limite:
E o enunciado pede pra a gente aplicar a definição 2 de limite no limite acima, achando os valores de para a e . Vamos então relembrar a definição de limite:
Se para todo número houver um número tal que:
Se então
Vamos reescrever essas condições sem os módulos e substituir nossas condições pra ficar mais fácil de visualizar:
Agora, bora colocar a mão na massa?
Passo 2
Para , a definição de um limite requer que ache um tal que
Somando em cada parcela da inequação:
Agora a gente precisa achar que corresponde a e . Para isso vamos plotar o gráfico e procurar:
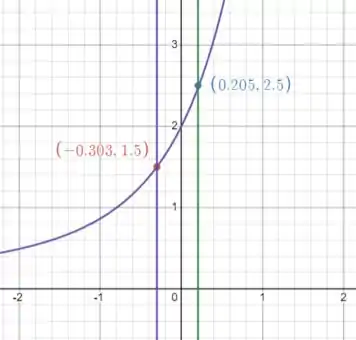
Dessa forma podemos dizer que:
Lembrando que:
Assim:
Substituindo os dois casos, temos:
Então já que esse é o único que respeita o nosso intervalo .
Passo 3
Agora, para , a definição de um limite requer que ache um tal que
Somando em cada parcela da inequação:
Agora a gente precisa achar que corresponde a e . Vamos procurar no gráfico:
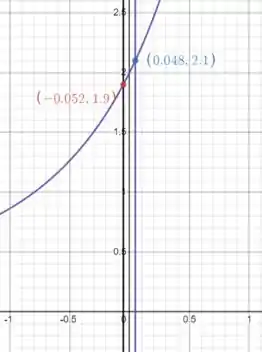
Dessa forma podemos dizer que:
Assim:
Pegamos então o menor ,
porque a gente tem certeza que ele vai encaixar no nosso intervalo!