Enunciado
Cálculo - Cálculo Volume 2 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 11.1 - Ex. 16
Liste os primeiros nove termos da sequência
Essa sequência parece ter um limite? Em caso afirmativo, encontre-o. Em caso negativo, explique por quê.
Passo 1
Fala aí!! Vamos entender o que essa questão quer? Nessa questão precisamos analisar se a sequência dada no enunciado parece ter um limite e, caso pareça ter, tentar encontrar esse limite ou justificar se não existir. Beleza?
A sequência do enunciado é
Então bora lá!
Passo 2
Primeiro vamos calcular os nove primeiros termos da sequência pra entender melhor qual é o comportamento de cada termo?
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Para :
Se calcularmos os trinta primeiros termos dessa sequência e plotarmos num gráfico, teremos:
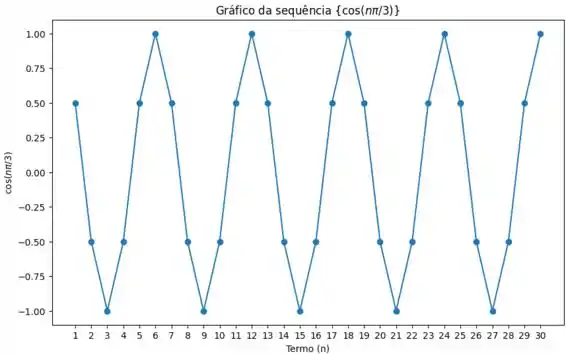
Se você reparar, os valores de não parecem tender a nenhum número, parecem mais como um ciclo que se repete.
Passo 3
Agora precisamos determinar o limite se ele existir. Se você reparar, A sequência oscila entre e repetidamente à medida que aumenta. Isso ocorre porque a função cosseno oscila entre e enquanto aumenta. Ou seja, os valores de não parecem tender a nenhum número, parecem mais como um ciclo que se repete. Isso acontece porque o cosseno é uma função periódica, então nunca vai existir um limite pra essa função quando , beleza?
Resposta
não existe, pois cosseno é uma função periódica