Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.3 - Ex. 52
Seja
- Determine as quantidades a seguir, se existirem.
- Esboçe o gráfico de .
Passo 1
Eaee, belezinha?? Bom... a questão nos dá a seguinte função:
Queremos calcular os seguintes limites:
Para isso, devemos aplicar conceitos de limites laterais.
Lembrando que os limites laterais descrevem como uma função se comporta à medida que a variável de entrada se aproxima de um valor específico a partir de um lado particular.
Existem dois tipos principais: o limite lateral direito (quando a variável se aproxima pelo lado direito) e o limite lateral esquerdo (quando a variável se aproxima pelo lado esquerdo).
Quando um limite em um ponto existe, significa dizer que os limites laterais nesse ponto são iguas!! 😉
Em outras palavras, um limite do tipo existe quando o limite lateral direito e o limite lateral esquerdo existem e são iguais!!
Agora bora aplicar!! 😉
Passo 2
Vamos calcular o limite
Como o limite tende a pela esquerda, devemos usar o (pois essa função é válida para todo ), assim:
Passo 3
Então pessoal , nós precisamos calcular o limite :
Para isso devemos calcular se os limites laterais são iguais , ou seja :
Primeiramente bora calcular o limite lateal direito:
Temos que , como o limite tende a pela direita, devemos usar o (pois essa função é válida para todo ), assim:
Logo, percebemos que os limites laterais são iguais, ou seja:
Sendo assim , podemos afirmar que:
Reparem que apesar de sabermos que , calculamos que o limite da função quando é dado por.
Simmmm , isso pode acontecer!!!!! Nesses casos dizemos que a função é descontínua nesse ponto.
Passo 4
Para calcular
é necessário apenas olhar nas limitações da função, assim:
Passo 5
Vamos calcular
Como o limite tende a pela esquerda, devemos usar o (pois essa função é válida para todo ), assim:
Passo 6
Vamos calcular
Como o limite tende a pela direita, devemos usar o (pois essa função é válida para todo ), assim:
Passo 7
O limite
não existe, pois seus limites laterais são diferentes:
Passo 8
Vamos agora esboçar o gráfico de .
É só substituir os valores correspondentes a cada intervalo dado
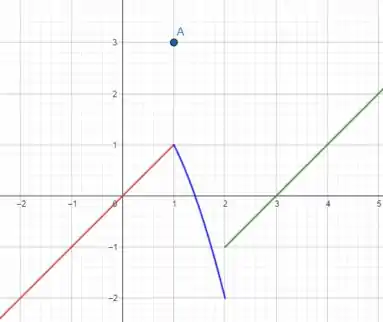
Onde:
- A reta vermelha refere-se a . Perceba que seu intervalo no gráfico é de ;
- O ponto refere-se a ;
- A curva em azul regere-se a . Perceba que seu intervalo é ;
- A curva em verde refere-se a . Perceba que seu intervalo no gráfico é de .
Resposta
(i)
(ii)
(iii)
(iv)
(v)
(vi) não existe
b)
