Como f x = log x ⁡ 2 se compara com g x = log 2 ⁡ x ? Eis aqui uma forma de saber. Use a equação log a ⁡ b= ln ⁡ bln ⁡ a para expressar f ( x ) e g ( x ) em termos de logaritmos naturais. Trace, em um mesmo gráfico, f e g . Comente o comportamento de f em relação aos sinais e valores de g .

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 7.Exercícios Práticos - Ex. 30

Como se compara com Eis aqui uma forma de saber.

Use a equação para expressar e em termos de logaritmos naturais.

Trace, em um mesmo gráfico, e . Comente o comportamento de em relação aos sinais e valores de .

Passo 1

Para resolver essas questões basta seguirmos o que ela nos recomenda em cada item e analisar o que nos é pedido. Assim, aplicando o logaritmo natural em e em teremos

Passo 2

Agora, plotando ambas as funções em um mesmo gráfico, vamos obter

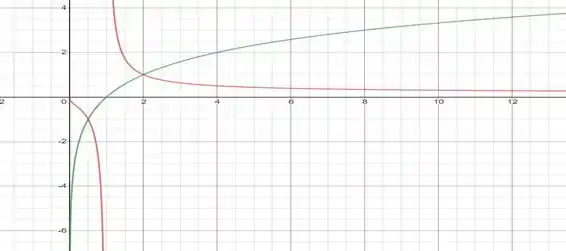
É possível observar que a função em verde é crescente onde a função está decrescendo.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o gráfico de y = log 2 ⁡ x seja feito sobre uma malha coordenada onde a unidade de comprimento deja 1 centímetro. Quantos quilômetros à direita da origem devemos percorrer antes de a altur

Use a Fórmula 10 para fazer o gráfico das funções dadas em uma mesma tela. Como se relacionam esses gráfico? y = ln ⁡ x ,y = log 10 ⁡ x , y = e x , y = 10 x

Use a Fórmula 10 para fazer o gráfico das funções dadas em uma mesma tela. Como se relacionam esses gráfico? y = log 1,5 ⁡ x , y = ln ⁡ x , y = log 10 ⁡ x , y = log 50 ⁡ x

Resolva cada equação em x :a) 2 ln x = 1 b) e^(- x) = 5

Resolva cada questão em x e^(2 x + 3) - 7 = 0 ln (5 - 2 x) = - 3