Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 34
- O que é o logaritmo natural?
- O que é o logaritmo comum?
- Esboce os gráficos, no mesmo sistema de coordenadas, das funções logaritmo natural e exponencial natural.
Passo 1
Falaeee, belezinha??? A questão nos faz três perguntinhas de forma direta a respeito dos logaritmos.
Para responder cada uma, devemos entender bem o conceito de logaritmo.
A gente sabe que um logaritmo é uma função matemática que descreve a relação entre um número, chamado de argumento do logaritmo, e uma base específica.
Em outras palavras, o logaritmo é o expoente ao qual a base deve ser elevada para produzir o número dado.
De forma geral, um logaritmo é expresso da seguinte forma:
Onde é a base, é o argumento e é o expoente para o qual deve ser elevado para obter .
E aí? Já dá pra responder? Bora junto!!
Passo 2
A primeira pergunta é sobre o que é um logaritmo natural.
Bom... O logaritmo natural é a função logarítmica com base em , é representado por ... ou seja:
Isso significa que .
Passo 3
Para a segunda pergunta queremos entender o que é um logaritmo comum.
Bom... O logaritmo comum é a função logarítmica com base em , é representado por , ou seja:
Isso significa que .
Passo 4
Por fim, a questão nos pede para esboçar no mesmo sistema de coordenadas, as funções logaritmo natural e exponencial natural:
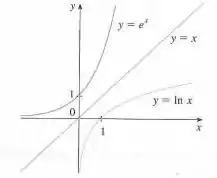
Aqui, temos que essas funções são simétricas em relação à reta da bissetriz, como na figura. Isso significa que elas são funções inversas.
Resposta
- O logaritmo natural é a função logarítmica com base em
- O logaritmo comum é a função logarítmica com base em .
