Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.1 - Ex. 17
Os lucros de uma pequena empresa em cada um de seus cinco primeiros anos de operação são dados na tabela a seguir:
- Trace pontos que representem o lucro em função do ano e os uma com a curva mais lisa possível.
- Qual é a taxa média de crescimentos dos lucros entre e ?
- Utilize o gráfico para estimar a taxa em que os lucros variaram em .
Passo 1
Primeira coisa que a gente tem que fazer é marcar esses pontos no plano cartesiano pra ver que curva que pode servir ali.
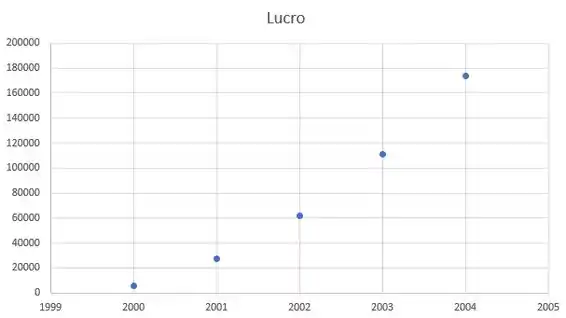
Concorda comigo que tá com a maior cara de parábola? Então vamos traçar uma linha que pareça com uma parábola ali! Vou botar o como sendo o , pra poder facilitar as contas. A parábola vai ter equação:
Passo 2
A gente vai medir a taxa de variação entre esses anos do jeito simplesmente dividindo a variação pelo tempo que passou:
A taxa vai ser de reais de lucro por ano.
Passo 3
A gente calcula a variação em um certo ano pela derivada da função naquele ponto. Vai ficar assim, ó:
A nossa parábola que representa o lucro é
E então, a variação do lucro vai ser:
Por isso, no ano de (que é o ano no nosso modelo), a variação vai ser:
Ou seja, temos variação de de lucro em .
Resposta
Ei, a resposta está no passo a passo :)