Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.6 - Ex. 2

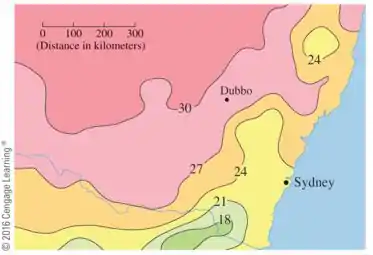
O mapa de contorno mostra a temperatura máxima média para novembro de (em ). Estimar o valor da derivada direcional desta função de temperatura em Dubbo, Nova Gales do Sul, na direção de Sydney. Quais são as unidades?

Passo 1

Oie, vamos resolver essa atividade?

Veja que temos aqui uma situação onde o mapa de contorno é mostrado abaixo, nele a gente tem as temperaturas máximas media para novembro de .

A gente quer então estimar o valor da derivada direcional da função de temperatura, em Dubbo.

Podemos aproximar a derivada direcional da função Temperatura em Dubbo, Novo Sul na direção de Sidney pela taxa média de variação de Temperatura entre os pontos onde a linha reta entre as cidades cruza diferentes zonas de temperatura.

Na direção de Sidney, a temperatura muda de 30 graus para 24 graus e usando a escala dada a distância entre essas duas cidades é de 350 km.

Passo 2

Analisando o mapa, temos que a região em que se encontra a cidade de Dubbo possui fronteira com as curvas de nível correspondentes a e .

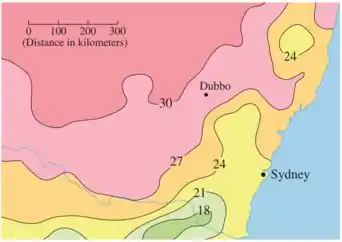
Como o mapa não possui escala, vamos utilizar a mesma da questão anterior. Com isso:

Temos então que:

Calculando então a nossa derivada direcional:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcular, usando a definição, a derivada direcional do campo escalar f ( x ,y ) no ponto indicado e na direção v → = i → + j → .c) f x ,y = e x + y em P 0 ,1 .

Nos exercícios de 2 a 6, calcular, usando a definição, a derivada direcional no ponto e direção indicados. 2 )f x ,y = x 2 - y 2 , P 1 ,2n ad i r e ç ã od e çã v → = 2 i → + 2 j → .

Calcular, usando a definição, a derivada direcional do campo escalar f ( x ,y ) no ponto indicado e na direção v → = i → + j → .b) f x ,y = 2 x + y em P - 1 ,2 .

Nos exercícios de 2 a 6, calcular, usando a definição, a derivada direcional no ponto e direção indicados. 4 )f x ,y = 2 x + 3 y , P - 1 ,2n ad i r e ç ã od ar e t ay = 2 x çã .

Calcular, usando a definição, a derivada direcional do campo escalar f ( x ,y ) no ponto indicado e na direção v → = i → + j → . f x ,y = 2 x 2 + 2 y 2 em P 1 ,1 .