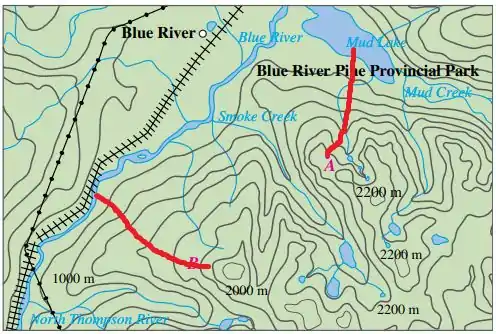
Um mapa topográfico de Blue River Pine Provincial Park em British Columbia é mostrado. Desenha as curvas da descida mais íngreme do ponto (descendo até o Mud Lake) e do ponto .
Passo 1
O problema fornece o seguinte mapa topográfico
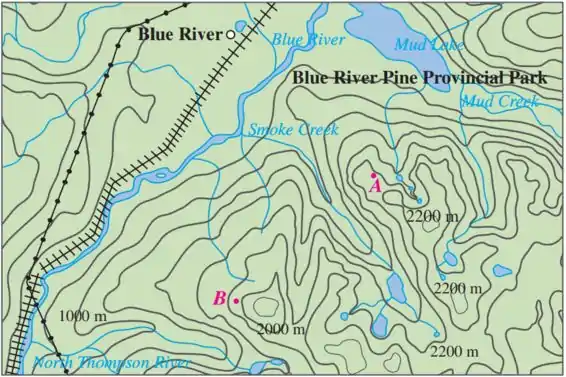
Que contém as curvas de nível que representam a altitude de cada ponto.
Em seguida o problema pede para desenharmos, partindo dos pontos e , as curvas de descida mais íngremes.
Para isso, temos que lembrar que a curva de descida mais íngreme será determinada pelo gradiente da função em cada ponto, pois ele determina a direção de maior crescimento e decrescimento.
E como o gradiente é perpendicular às curvas de nível, temos que traçar uma curva que parte dos pontos dados e é sempre perpendicular as curvas de nível.
Representando essa perpendicularidade visualmente temos o seguinte
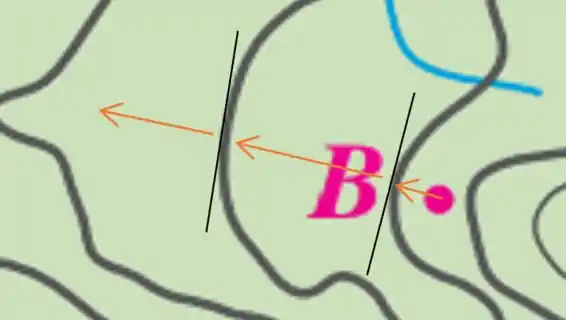
Onde saímos do ponto , chegamos na curva de nível e traçamos uma “reta tangente” ao ponto que chegamos. Dessa “reta tangente” nós partimos para a próxima curva de nível na direção perpendicular à “reta tangente” e assim por diante.
Passo 2
Fazendo isso, obtemos
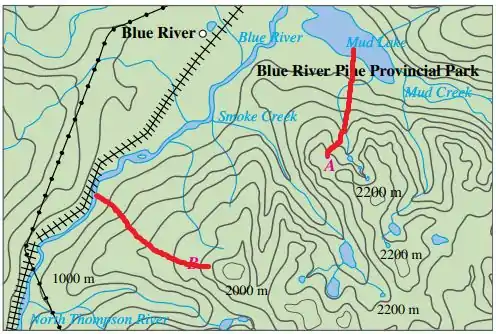
Resposta